Ania wycięła z kartki papieru dwa jednakowe trójkąty prostokątne o bokach długości \(12cm\), \(16cm\) i \(20cm\). Pierwszy z nich zagięła wzdłuż symetralnej krótszej przyprostokątnej, a drugi - wzdłuż symetralnej dłuższej przyprostokątnej. W ten sposób otrzymała czworokąty pokazane na rysunkach.





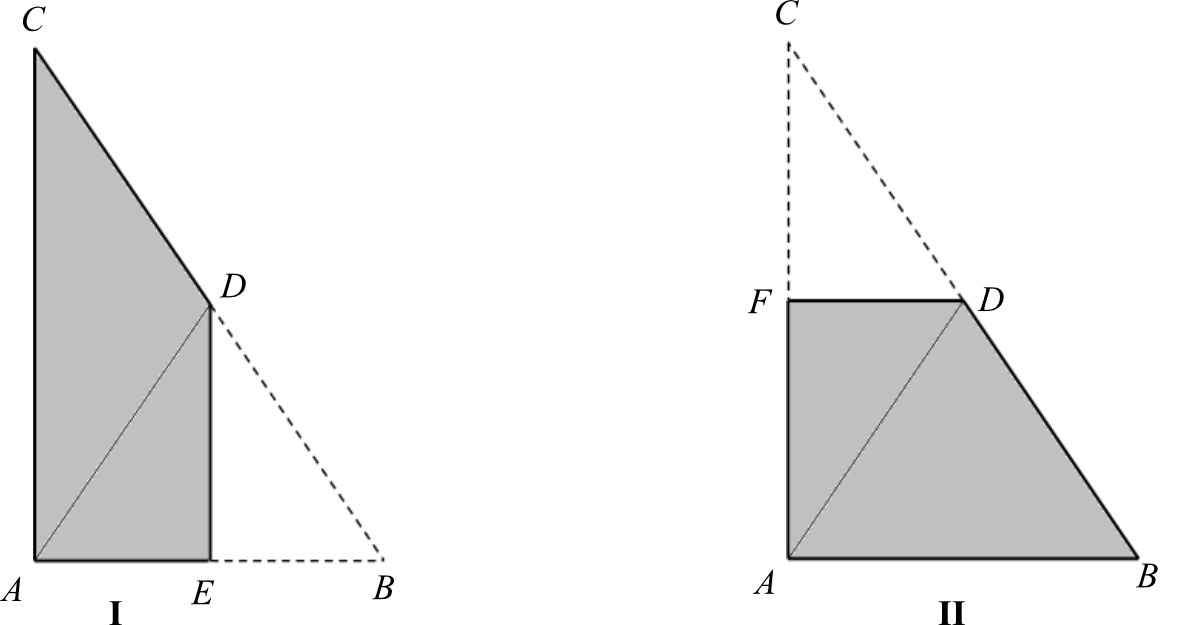
Oceń prawdziwość podanych zdań. Pole czworokąta I jest równe polu czworokąta II.
Obwód czworokąta I jest mniejszy od obwodu czworokąta II.

Pole czworokąta I jest równe polu czworokąta II.

Odpowiedź:      

1) PRAWDA

2) FAŁSZ

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Nanieśmy na obydwa rysunki odpowiednie miary, które występują w treści zadania: Teraz zgodnie z treścią zadania musimy obliczyć pola oraz obwody obydwu trapezów, mając tak naprawdę wszystkie podane miary. Krok 2. Obliczenie pola i obwodu pierwszego trapezu. Zacznijmy od pola powierzchni. Nasz trapez jest nieco przekręcony, ale jego podstawy mają długość \(16cm\) oraz \(8cm\), natomiast wysokość jest równa \(6cm\), zatem: $$P=\frac{a+b}{2}\cdot h \           ,\ P=\frac{16+8}{2}\cdot6 \           ,\ P=\frac{24}{2}\cdot6 \           ,\ P=12\cdot6 \           ,\ P=72[cm^2]$$ Obwód pierwszego trapezu jest natomiast równy: $$Obw=6+8+10+16=40[cm]$$ Krok 3. Obliczenie pola i obwodu drugiego trapezu. Teraz obliczmy te same dane dla drugiego trapezu. Tym razem nasz trapez ma podstawy równe \(12cm\) oraz \(6cm\), natomiast wysokość jest równa \(8cm\), zatem pole powierzchni będzie równe: $$P=\frac{a+b}{2}\cdot h \           ,\ P=\frac{12+6}{2}\cdot8 \           ,\ P=\frac{18}{2}\cdot8 \           ,\ P=9\cdot8 \           ,\ P=72[cm^2]$$ Obwód tego drugiego trapezu będzie natomiast równy: $$Obw=12+10+6+8=36cm$$ Krok 4. Ocena prawdziwości obydwu zdań. Zgodnie z naszymi obliczeniami pola powierzchni obydwu trapezów są sobie równe, zatem pierwsze zdanie jest prawdą. Obwody trapezów są natomiast różne, co oznacza że drugie zdanie jest fałszem.

Teoria:      
W trakcie opracowania