Zbiory arkuszy egzaminacyjnych z matematyki dla ósmoklasistów. Znajdziesz tu różnorodne zadania egzaminacyjne, przykładowe arkusze, rozwiązania zadań, testy z matematyki oraz wiele innych przydatnych materiałów
Egzamin gimnazjalny 2015 - matematyka Zadanie 20 z 23
Zadanie nr 20. (1pkt)
Na rysunku przedstawiono ostrosłup prawidłowy czworokątny i sześcian. Bryły mają jednakowe podstawy i równe wysokości, a suma objętości tych brył jest równa \(36cm^3\).
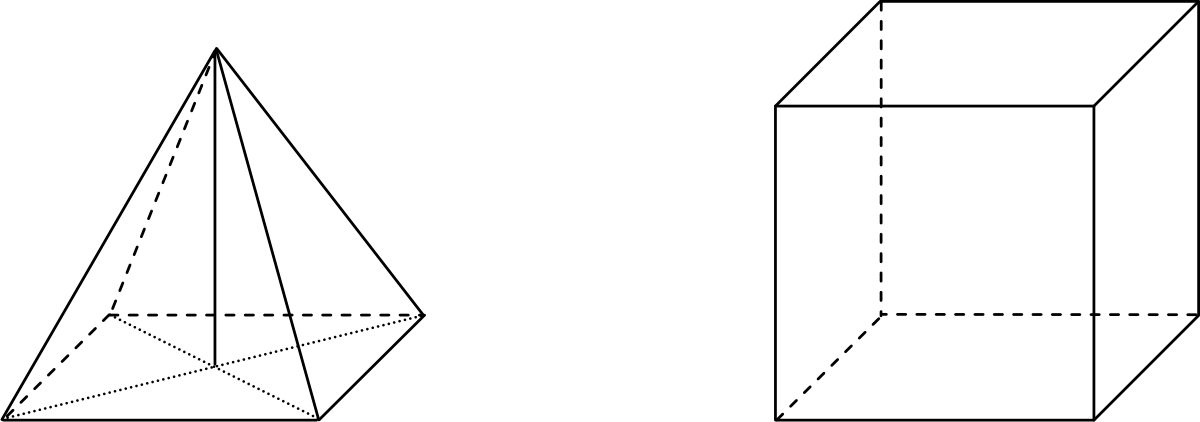
Oceń prawdziwość podanych zdań. Objętość sześcianu jest trzy razy większa od objętości ostrosłupa.
Krawędź sześcianu ma długość \(3cm\).
Objętość sześcianu jest trzy razy większa od objętości ostrosłupa.
Odpowiedź:
1) PRAWDA
2) PRAWDA
Rozwiązanie:
Krok 1. Ocena prawdziwości pierwszego zdania.
Zapiszmy sobie wzory na objętość ostrosłupa oraz sześcianu.
$$V_{ostrosłupa}=\frac{1}{3}P_{p}\cdot H \ ,\
V_{sześcianu}=P_{p}\cdot H$$
Z treści zadania wiemy, że pola podstaw oraz wysokości są takie same w obydwu bryłach. Skoro tak, to faktycznie objętość sześcianu będzie trzykrotnie większa od objętości ostrosłupa, a wynika to wprost ze wzorów na objętość tych brył. To oznacza, że pierwsze zdanie jest prawdą.
Krok 2. Ocena prawdziwości drugiego zdania.
Suma objętości tych dwóch brył jest równa \(36cm^3\). W poprzednim kroku udowodniliśmy sobie, że objętość sześcianu będzie \(3\) razy większa od objętości ostrosłupa. Jeżeli więc objętość ostrosłupa oznaczymy jako \(x\), to objętość sześcianu wyniesie \(3x\). Możemy zatem zapisać, że:
$$x+3x=36cm^3 \ ,\
4x=36cm^3 \ ,\
x=9cm^3$$
To oznacza, że nasz sześcian ma objętość:
$$3x=3\cdot9cm^3=27cm^3$$
Objętość sześcianu obliczamy ze wzoru \(V=a^3\), a skoro ta objętość wynosi \(27cm^3\), to otrzymamy równanie:
$$V=a^3 \ ,\
27cm^3=a^3 \ ,\
a=3cm$$
To oznacza, że drugie zdanie jest prawdą.
Teoria:
W trakcie opracowania
CKE

