Na rysunku przedstawiono sześciokąt foremny o boku równym \(2cm\). Przekątna \(AD\) dzieli go na dwa przystające trapezy równoramienne.





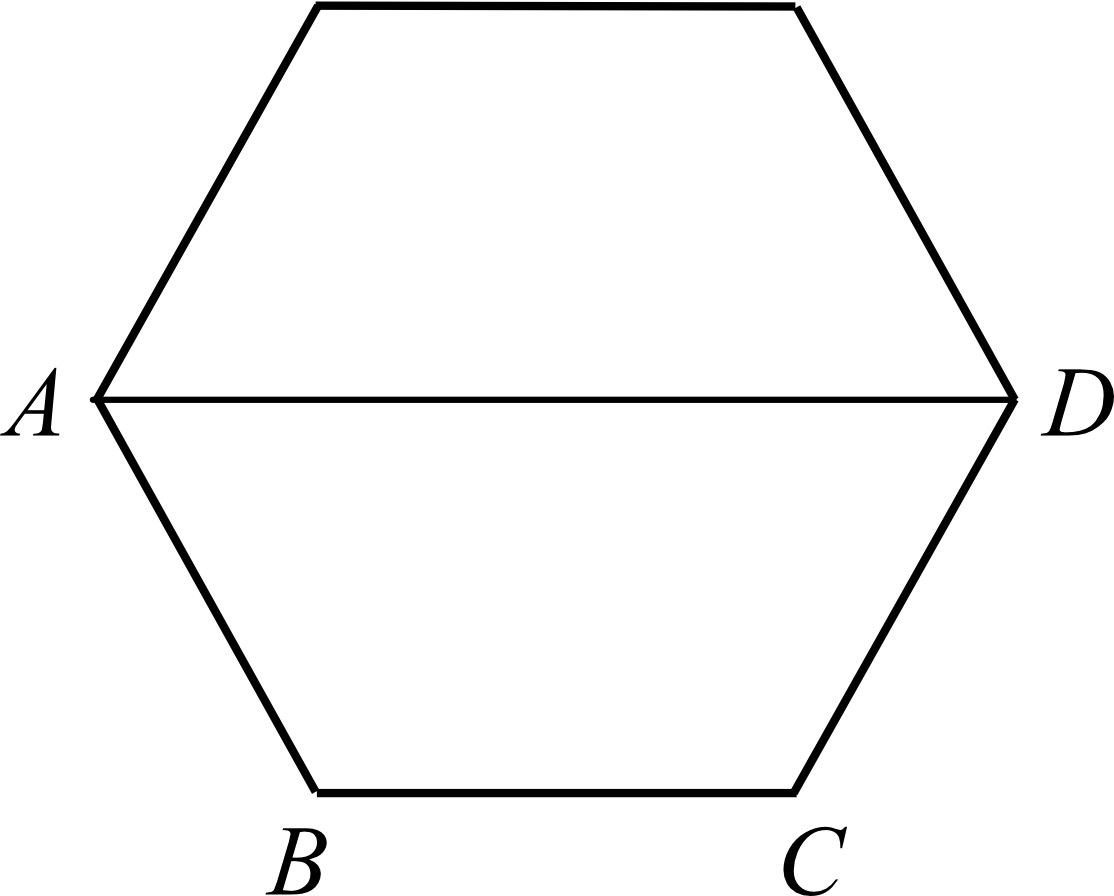
Wysokość trapezu \(ABCD\) jest równa:

A \(\sqrt{2}cm\)
B \(\frac{\sqrt{3}}{2}cm\)
C \(\sqrt{3}\)
D \(2cm\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Ustalenie miary kątów wewnętrznych sześciokąta. Aby rozwiązać to zadanie musimy wiedzieć, że każdy kąt wewnętrzny sześciokąta foremnego ma miarę \(120°\). Skąd to wiemy? Najprościej będzie to zapamiętać w ten sposób, że począwszy od trójkąta mamy następującą zależność jeśli chodzi o sumę kątów wewnętrznych: Trójkąt - \(180°\) Czworokąt - \(360°\) Pięciokąt - \(540°\) Sześciokąt - \(720°\) Krótko mówiąc, z każdym kolejnym dodatkowym kątem figura ma sumę kątów wewnętrznych o \(180°\) większą. My wiemy, że nasz sześciokąt jest foremny, a to oznacza że miary jego kątów są identyczne. Zatem miara pojedynczego kąta będzie równa po prostu: $$720°:6=120°$$ Krok 2. Sporządzenie rysunku pomocniczego. Mając informacje z kroku pierwszego oraz z treści zadania zróbmy sobie mały rysunek pomocniczy, na którym przy okazji zaznaczymy poszukiwaną wysokość trapezu. Kąt \(CDE\) ma na pewno miarę równą \(120°:2=60°\), bo prosta \(AD\) podzieliła nam jeden z kątów wewnętrznych na dwie równe części. Wysokość trójkąta pada zawsze pod kątem \(90°\), a to z kolei oznacza że nasz trójkąt \(CDE\) jest klasycznym trójkątem o mierze kątów \(30°, 60°, 90°\). Dzięki temu możemy sobie oznaczyć poszczególne długości przyprostokątnych jako \(a\), \(a\sqrt{3}\) oraz przeciwprostokątną jako \(2a\). Krok 3. Wykorzystanie własności trójkąta i wyznaczenie wysokości trapezu. Znamy długość boku \(CD\) i jest ona równa \(2cm\). Skoro tak, to zgodnie z własnościami trójkątów \(30°, 60°, 90°\) odcinek \(ED\) będzie dwukrotnie krótszy, czyli będzie miał długość \(a=1cm\), a interesujący nas odcinek \(EC\) będący wysokością trójkąta będzie mieć miarę \(a\sqrt{3}\), czyli \(1\cdot\sqrt{3}cm=\sqrt{3}cm\).

Teoria:      
W trakcie opracowania