Dany jest ośmiokąt foremny wpisany w okrąg \(K\). Punkty \(A\) oraz \(B\) są sąsiednimi wierzchołkami tego ośmiokąta oraz \(\alpha\) jest kątem między styczną do okręgu \(K\) w punkcie \(A\) i bokiem \(AB\) wielokąta (zobacz rysunek).





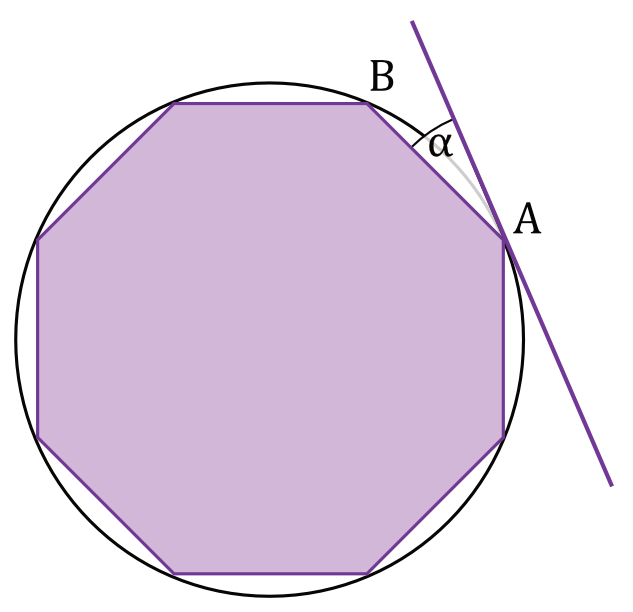
Miara kąta \(\alpha\) jest równa:

A \(45°\)
B \(30°\)
C \(22,5°\)
D \(15°\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Powinniśmy zwrócić uwagę, że boki ośmiokąta (w tym ten, który jest przy naszym kącie \(\alpha\)) są cięciwami okręgu, który jest opisany na tej figurze. Z twierdzenia o mierze kąta między styczną a cięciwą wynika, że miara naszego kąta \(\alpha\) jest równa mierze kąta wpisanego, który oparty byłby na łuku \(AB\). Dobrze to będzie widać na poniższym rysunku: Na rysunku pomocniczym pojawił się też kąt \(\beta\). który jest kątem środkowym opartym na łuku \(AB\). Zgodnie z własnościami kątów wpisanych i środkowych, miara tego jest dwa razy większa od miary poszukiwanego kąta \(\alpha\). Krok 2. Obliczenie miary kąta \(\beta\). Miara kąta środkowego \(\beta\) stanowi \(\frac{1}{8}\) kąta pełnego (ponieważ nasza figura jest ośmiokątem foremnym), zatem: $$\beta=\frac{360°}{8} \           ,\ \beta=45°$$ Krok 3. Obliczenie miary kąta \(\alpha\). Kąt \(\alpha\) stanowi połowę miary kąta \(\beta\), zatem: $$\alpha=\frac{1}{2}\cdot45° \           ,\ \alpha=22,5°$$

Teoria:      
W trakcie opracowania