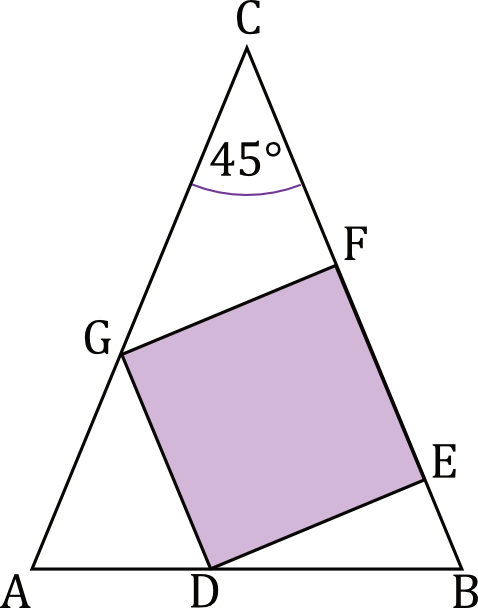
Dane są trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|\) i \(|\sphericalangle ACB|=45°\), oraz kwadrat \(DEFG\) o polu równym \(1\). Wierzchołki \(E\) i \(F\) kwadratu leżą na ramieniu \(BC\) danego trójkąta, wierzchołek \(G\) leży na ramieniu \(AC\), a wierzchołek \(D\) leży na podstawie \(AB\) trójkąta (zobacz rysunek).





Oceń prawdziwość poniższych relacji. Wybierz P, jeśli relacja jest prawdziwa, albo F – jeśli jest fałszywa. \(|\sphericalangle AGD|=45°\)
\(|AG|-|BE|=2-\sqrt{2}\)

\(|\sphericalangle AGD|=45°\)

Odpowiedź:      

1) PRAWDA

2) PRAWDA

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Kluczem do sukcesu jest dostrzeżenie, że odcinek \(DG\) jest równoległy do ramienia \(BC\) (ponieważ boki kwadratu są względem siebie równoległe). Mówiąc bardzo obrazowo, mamy tutaj tak naprawdę standardową sytuację znaną z trójkątów podobnych, co dobrze będzie widać na poniższym rysunku: Można więc wysnuć wniosek, że trójkąt \(ADG\) jest trójkątem podobnym do trójkąta równoramiennego \(ABC\), czyli tym samym trójkąt \(ADG\) jest także równoramienny. Krok 2. Ocena prawdziwości pierwszego zdania. Skoro ustaliliśmy już, że trójkąty \(ADG\) oraz \(ABC\) są podobne, to znaczy, że będą miały one tą samą miarę kąta między ramionami. To prowadzi nas do wniosku, że kąt \(AGD\) ma \(45°\), zatem zdanie jest prawdą. Krok 3. Ocena prawdziwości drugiego zdania. Wiemy, że kwadrat \(DEFG\) ma pole równe \(1\), czyli tym samym każdy bok tego kwadratu ma długość \(1\), ponieważ \(P=1^2=1\). Spójrzmy teraz na trójkąt \(GFC\). Jest to trójkąt prostokątny, a skoro jeden z jego kątów ma miarę \(45°\), to jest to tak naprawdę jeszcze trójkąt równoramienny (tzw. połówka kwadratu). To prowadzi nas do wniosku, że tym samym \(|FC|=1\). Dodatkowo zgodnie z własnościami trójkątów o kątach \(45°,45°,90°\) możemy stwierdzić, że \(|GC|=\sqrt{2}\). Długości ramion \(AC\) oraz \(BC\) są sobie równe, stąd też zgodnie z rysunkiem możemy zapisać, że: $$|AC|=|BC| \           ,\ |AG|+\sqrt{2}=|BE|+1+1\           ,\ |AG|-|BE|+\sqrt{2}=2 \           ,\ |AG|-|BE|=2-\sqrt{2}$$

Teoria:      
W trakcie opracowania