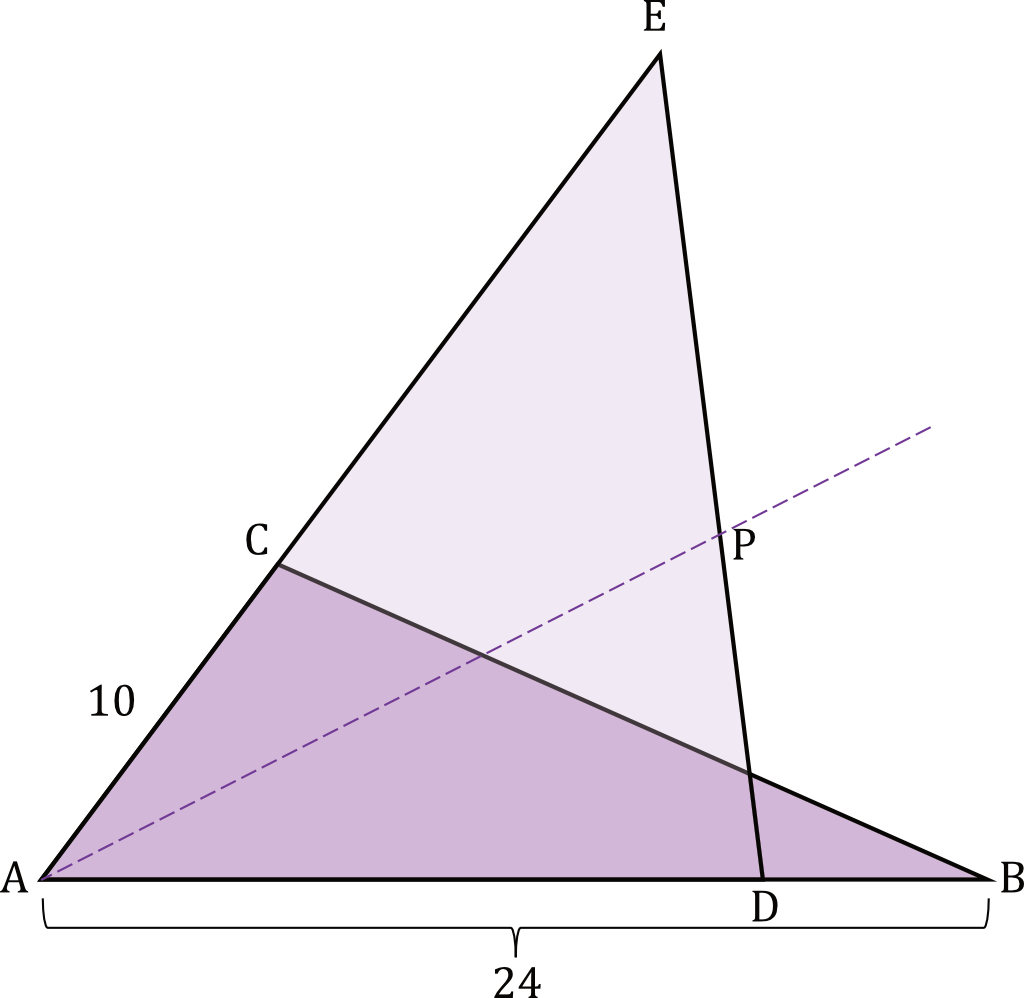
Dane są dwa trójkąty \(ABC\) i \(ADE\) o wspólnym kącie ostrym przy wierzchołku \(A\). Ponadto \(|AB|=24\), \(|AC|=10\) (zobacz rysunek). Pole trójkąta \(ADE\) jest dwukrotnie większe od pola trójkąta \(ABC\).
Zadanie 1.
Dwusieczna kąta \(BAC\) przecina odcinek \(DE\) w punkcie \(P\), takim że \(\frac{|DP|}{|PE|}=\frac{3}{4}\). Oblicz długości boków \(AD\) i \(AE\) trójkąta \(ADE\).
Zadanie 2.
Pole trójkąta \(ABC\) jest równe \(72\). Oblicz długość boku \(BC\) trójkąta \(ABC\).
Odpowiedź:
1. \(|AE|=8\sqrt{10}\) oraz \(|AD|=6\sqrt{10}\)
2. \(|BC|=\sqrt{4\cdot73}=2\sqrt{73}\)
Rozwiązanie:
Rozwiązanie 1.
Krok 1. Zapisanie równań.
Z treści zadania wynika, że pole trójkąta \(ADE\) jest dwukrotnie większe od pola trójkąta \(ABC\), czyli:
$$P_{ADE}=2\cdot P_{ABC}$$
Przyjmijmy, że kąt \(BAC\) oznaczymy jako \(\alpha\). W takim razie, korzystając ze wzoru na pole powierzchni trójkąta "z sinusem", możemy zapisać, że:
$$\frac{1}{2}\cdot|AD|\cdot|AE|\cdot sin\alpha=2\cdot\frac{1}{2}|AB|\cdot|AC|\cdot sin\alpha \quad\bigg/:sin\alpha \ ,\
\frac{1}{2}\cdot|AD|\cdot|AE|=|AB|\cdot|AC|$$
Podstawiając teraz znane z treści zadania długości boków, czyli \(|AB|=24\) oraz \(|AC|=10\), otrzymamy:
$$\frac{1}{2}\cdot|AD|\cdot|AE|=24\cdot10 \ ,\
\frac{1}{2}\cdot|AD|\cdot|AE|=240 \quad\bigg/\cdot2 \ ,\
|AD|\cdot|AE|=480$$
Krok 2. Zapisanie zależności wynikającej z twierdzenia o dwusiecznej kąta.
Spójrzmy na trójkąt \(ADE\). Z twierdzenia o dwusiecznej kąta \(BAC\) wynika, że skoro \(\frac{|DP|}{|PE|}=\frac{3}{4}\), to także \(\frac{|AD|}{|AE|}=\frac{3}{4}\). W związku z tym:
$$\frac{|AD|}{|AE|}=\frac{3}{4} \quad\bigg/\cdot |AE| \ ,\
|AD|=\frac{3}{4}|AE|$$
Krok 3. Obliczenie długości odcinka \(AE\).
Podstawiając teraz wyznaczoną długość \(|AD|\) do równania \(|AD|\cdot|AE|=480\), otrzymamy:
$$\frac{3}{4}|AE|\cdot|AE|=480 \quad\bigg/\frac{4}{3} \ ,\
|AE|^2=640 \ ,\
|AE|=\sqrt{640} \quad\lor\quad |AE|=-\sqrt{640}$$
Ujemny wynik oczywiście odrzucamy, bo długość boku musi być dodatnia. Zostaje nam więc \(|AE|=\sqrt{640}\), co możemy jeszcze rozpisać jako \(|AE|=\sqrt{64\cdot10}=8\sqrt{10}\).
Krok 4. Obliczenie długości odcinka \(AD\).
Na koniec została nam do obliczenia długość odcinka \(AD\). Korzystając z równania \(|AD|=\frac{3}{4}|AE|\), możemy zapisać, że:
$$|AD|=\frac{3}{4}\cdot8\sqrt{10} \ ,\
|AD|=6\sqrt{10}$$
Rozwiązanie 2.
Krok 1. Obliczenie wartości \(sin\alpha\).
Przyjmijmy, że kąt \(BAC\) oznaczymy jako \(\alpha\). W takim razie, korzystając ze wzoru na pole trójkąta "z sinusem", możemy zapisać, że:
$$P=\frac{1}{2}\cdot|AB|\cdot|AC|\cdot sin\alpha$$
Z treści zadania wiemy, że pole tego trójkąta jest równe \(72\) i wiemy, że \(|AB|=24\) oraz \(|AC|=10\) zatem:
$$72=\frac{1}{2}\cdot24\cdot10\cdot sin\alpha \ ,\
72=120\cdot sin\alpha \ ,\
sin\alpha=\frac{72}{120}=\frac{3}{5}$$
Krok 2. Obliczenie wartości \(cos\alpha\).
W tym zadaniu będziemy chcieli wykorzystać twierdzenie cosinusów, a póki co, znamy tylko wartość sinusa. Obliczmy zatem wartość cosinusa, a dokonamy tego korzystając z jedynki trygonometrycznej:
$$sin^2\alpha+cos^2\alpha=1 \ ,\
\left(\frac{3}{5}\right)^2+cos^2\alpha=1 \ ,\
\frac{9}{25}+cos^2\alpha=1 \ ,\
cos^2\alpha=\frac{16}{25} \ ,\
cos\alpha=\frac{4}{5} \quad\lor\quad cos\alpha=-\frac{4}{5}$$
Z treści zadania wynika, że kąt przy wierzchołku \(A\) jest ostry, a dla takich kątów cosinus przyjmuje jedynie dodatnie wartości, stąd też jedynym pasującym rozwiązaniem będzie \(cos\alpha=\frac{4}{5}\).
Krok 3. Obliczenie długości boku \(BC\).
Teraz możemy przejść do obliczenia długości boku \(BC\), czyli boku, który leży naprzeciwko naszego kąta \(\alpha\). W tym celu skorzystamy z twierdzenia cosinusów:
$$c^2=a^2+b^2-2ab\cdot cos\alpha$$
Kluczową sprawą jest tutaj to, aby pod \(c\) podstawić właśnie ten nasz poszukiwany bok \(BC\), bo to on jest naprzeciwko kąta \(\alpha\). Boki \(a\) oraz \(b\) to odpowiednio boki \(AB\) oraz \(AC\) o długości \(24\) oraz \(10\), natomiast \(cos\alpha=\frac{4}{5}\), zatem:
$$|BC|^2=24^2+10^2-2\cdot24\cdot10\cdot\frac{4}{5} \ ,\
|BC|^2=576+100-384 \ ,\
|BC|^2=292 \ ,\
|BC|=\sqrt{292} \quad\lor\quad |BC|=-\sqrt{292}$$
Ujemny wynik oczywiście odrzucamy, zatem zostaje nam jedynie \(|BC|=\sqrt{292}\), co możemy jeszcze rozpisać jako \(|BC|=\sqrt{4\cdot73}=2\sqrt{73}\).
Teoria:
W trakcie opracowania

