Dane są:

• okrąg o środku \(S\) i promieniu \(r=1\)

• prosta \(k\) przechodząca przez \(S\) i przecinająca okrąg w punktach \(P\) i \(Q\)

• prosta \(l\) styczna do danego okręgu w punkcie \(T\).



Prosta \(k\) przecina prostą \(l\) w punkcie \(R\). Prosta przechodząca przez punkt \(Q\) i równoległa do odcinka \(ST\) przecina styczną \(l\) w punkcie \(U\) (zobacz rysunek).





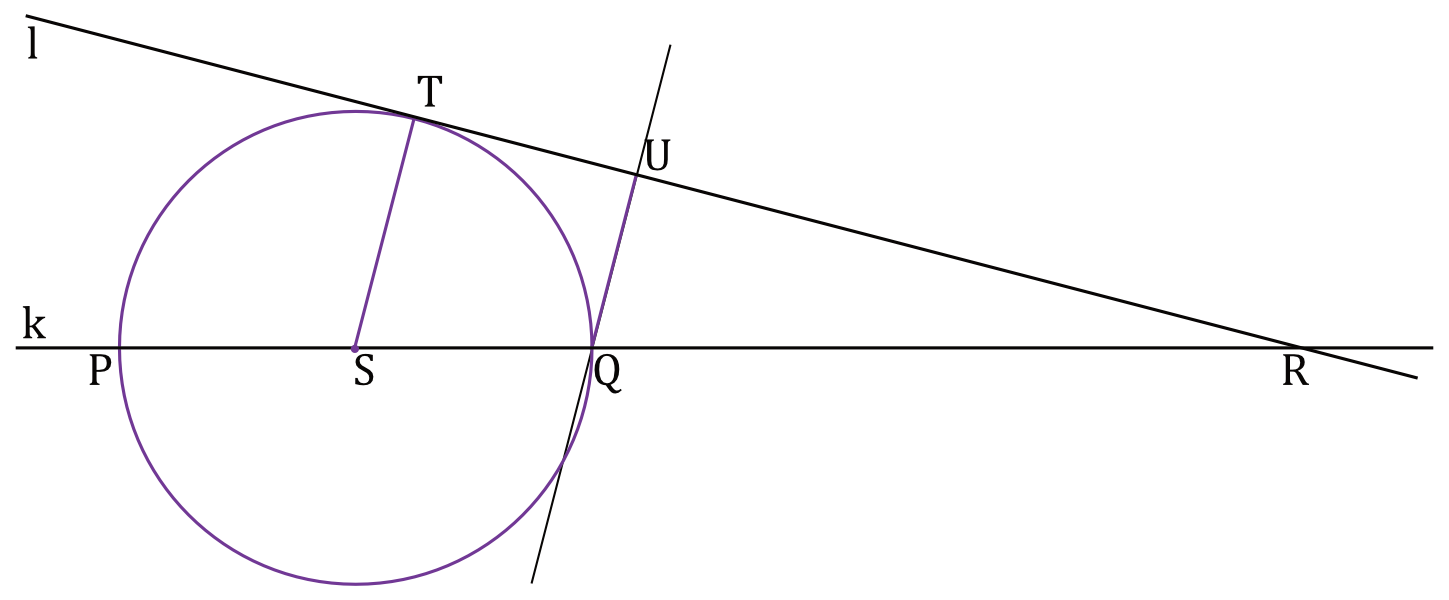
Oblicz długość odcinka \(TU\) wiedząc, że spełniony jest warunek \(\frac{|PQ|}{|QR|}=\frac{2}{3}\).

Odpowiedź:      

\(|TU|=\frac{\sqrt{15}}{4}\)

Rozwiązanie:      
Krok 1. Obliczenie długości odcinków \(QR\) oraz \(SR\). Wiemy, że promień okręgu ma długość \(r=1\). Odcinek \(PQ\) jest średnicą tego okręgu, czyli tym samym możemy zapisać, że: $$|PQ|=2\cdot1 \           ,\ |PQ|=2$$ W treści zadania mamy podaną informację, że zachodzi zależność opisana równaniem \(\frac{|PQ|}{|QR|}=\frac{2}{3}\). Skoro więc \(|PQ|=2\), to wniosek z tego płynie taki, iż \(|QR|=3\). Możemy też już policzyć długość odcinka \(SR\), ponieważ: $$|SR|=r+|QR| \           ,\ |SR|=1+3 \           ,\ |SR|=4$$ Krok 2. Obliczenie długości odcinka \(TR\). Spójrzmy na trójkąt \(STR\). Jest to trójkąt prostokątny, ponieważ z własności stycznych do okręgu wynika, że styczna do okręgu tworzy z promieniem kąt prosty. Skoro tak, to korzystając z twierdzenia Pitagorasa, możemy zapisać, że: $$|ST|^2+|TR|^2=|SR|^2 \           ,\ 1^2+|TR|^2=4^2 \           ,\ 1+|TR|^2=16 \           ,\ |TR|^2=15 \           ,\ |TR|=\sqrt{15} \quad\lor\quad |TR|=-\sqrt{15}$$ Długość odcinka musi być oczywiście dodatnia, stąd też zostaje nam jedynie \(|TR|=\sqrt{15}\). Krok 3. Obliczenie długości odcinka \(TU\). Korzystając z twierdzenia Talesa, możemy zapisać, że: $$\frac{|TU|}{|TR|}=\frac{|SQ|}{|SR|} \           ,\ \frac{|TU|}{\sqrt{15}}=\frac{1}{4} \           ,\ |TU|=\frac{\sqrt{15}}{4}$$

Teoria:      
W trakcie opracowania