W wycinek koła wyznaczony przez kąt środkowy \(KSL\) o mierze \(45°\) wpisano kwadrat \(ABCD\) w taki sposób, że wierzchołki \(A\) oraz \(B\) leżą na promieniu \(SK\), wierzchołek \(D\) leży na promieniu \(SL\), a wierzchołek \(C\) leży na łuku \(KL\) (zobacz rysunek).





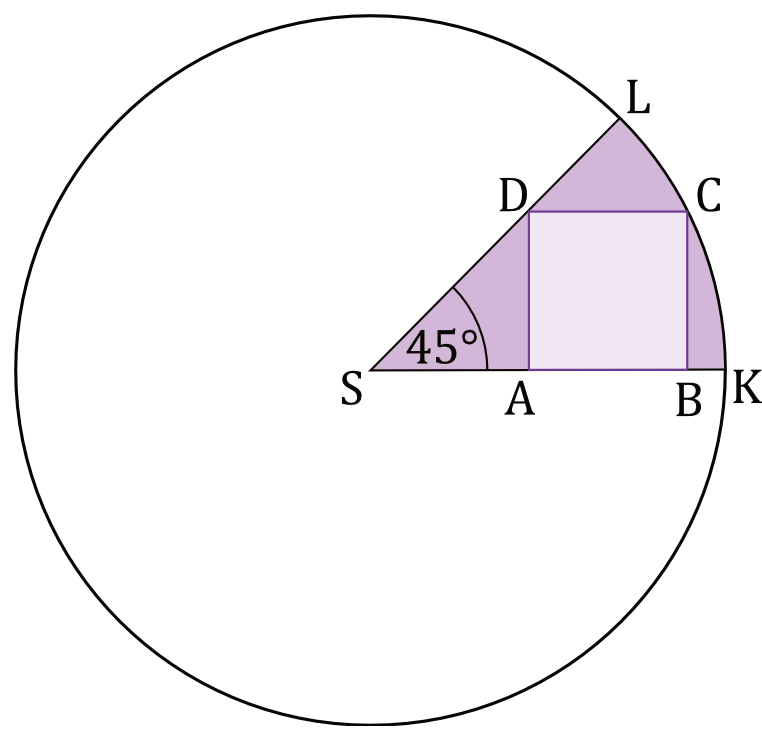
Oblicz stosunek pola kwadratu \(ABCD\) do pola wycinka kołowego \(KSL\).

Odpowiedź:      

\(\frac{8}{5\pi}\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Kluczem do sukcesu będzie połączenie punktu \(S\) z punktem \(C\), rysując w ten sposób promień okręgu, który jest jednocześnie przeciwprostokątną trójkąta \(SBC\). Dodatkowo jeżeli bok kwadratu oznaczymy jako \(a\), to powstanie nam taka oto sytuacja: Zwróćmy uwagę na trójkąt \(SAD\). Jest to trójkąt prostokątny, a skoro jeden z jego kątów ma miarę \(45°\), to będzie to w dodatku trójkąt równoramienny. To pozwala stwierdzić, że \(|SA|=a\), czyli tym samym \(|SB|=2a\). Krok 2. Obliczenie długości promienia. Spójrzmy na trójkąt \(SBC\). Jest to trójkąt prostokątny, w którym dolna przyprostokątna ma długość \(2a\), a boczna przyprostokątna ma długość \(a\). Przeciwprostokątną jest odcinek \(SC\), czyli promień okręgu. Skoro tak, to korzystając z twierdzenia Pitagorasa, możemy zapisać, że: $$(2a)^2+a^2=r^2 \           ,\ 4a^2+a^2=r^2 \           ,\ 5a^2=r^2 \           ,\ r=a\sqrt{5} \quad\lor\quad r=-a\sqrt{5}$$ Długość promienia musi być dodatnia, więc zostaje nam \(r=a\sqrt{5}\). Krok 3. Obliczenie pola powierzchni wycinka kołowego. Znamy długość promienia, więc możemy obliczyć pole całego koła: $$P=\pi r^2 \           ,\ P=\pi\cdot(a\sqrt{5})^2 \           ,\ P=\pi\cdot a^2\cdot5 \           ,\ P=5\pi\cdot a^2$$ Skoro kąt środkowy ma miarę \(45°\), to wycinek koła stanowi \(\frac{45°}{360°}=\frac{1}{8}\) pola całego koła. Możemy więc zapisać, że: $$P_{KSL}=\frac{1}{8}\cdot5\pi\cdot a^2 \           ,\ P_{KSL}=\frac{5}{8}\pi\cdot a^2$$ Krok 4. Obliczenie stosunku pól powierzchni. Na koniec musimy jeszcze obliczyć stosunek powierzchni pola kwadratu (tutaj \(P=a^2\)), względem pola wycinka \(KSL\) (tutaj \(P=\frac{5}{8}\pi\cdot a^2\)). Bardzo łatwo tutaj o pomyłkę, dlatego rozpiszmy to bardzo dokładnie: $$\frac{a^2}{\frac{5}{8}\pi\cdot a^2}=a^2:\frac{5}{8}\pi\cdot a^2=a^2\cdot\frac{8}{5\pi\cdot a^2}=\frac{8}{5\pi}$$

Teoria:      
W trakcie opracowania