Dane są liczby: \(a=2\sqrt{2}, b=4, c=4\sqrt{2}\).

Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie spośród 1., 2. albo 3.



Liczby \(a\), \(b\) oraz \(c\) tworzą w podanej kolejności:

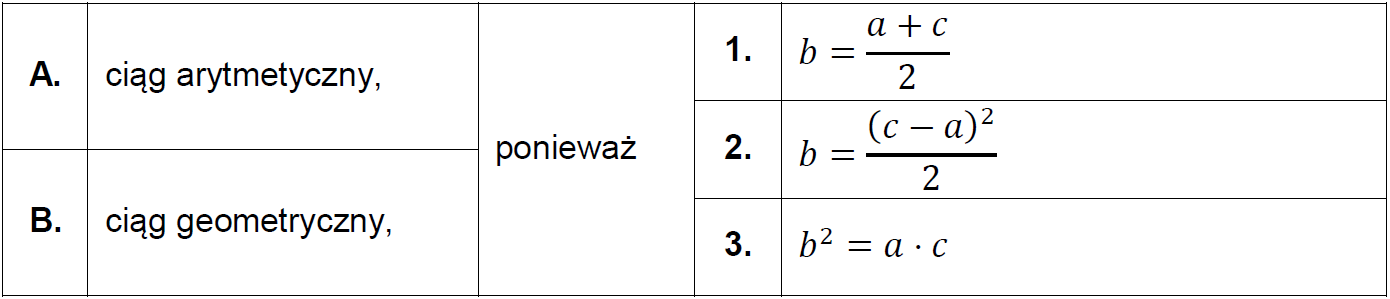
Odpowiedź:      

B., ponieważ 3.

Rozwiązanie:      
Jeżeli ten ciąg jest arytmetyczny, to zajdzie w nim bardzo charakterystyczna własność między trzema kolejnymi wyrazami, czyli: $$a_{2}=\frac{a_{1}+a_{3}}{2}$$ Z kolei jeśli ten ciąg jest geometryczny, to zajdzie w nim następująca własność: $${a_{2}}^2=a_{1}\cdot a_{3}$$ Sprawdźmy zatem, która z tych własności będzie spełniona, zaczynając od ciągu arytmetycznego. Podstawiając dane z treści zadania, otrzymamy: $$4=\frac{2\sqrt{2}+4\sqrt{2}}{2} \           ,\ 4=\frac{6\sqrt{2}}{2} \           ,\ 4=3\sqrt{2} \           ,\ L\neq P$$ Wyszła nam sprzeczność, czyli wiemy już, że ten ciąg nie jest arytmetyczny. To teraz sprawdźmy, czy jest geometryczny: $$4^2=2\sqrt{2}\cdot4\sqrt{2} \           ,\ 16=8\cdot2 \           ,\ 16=16 \           ,\ L=P$$ Taki wynik oznacza, że faktycznie ten ciąg jest geometryczny, ponieważ \(b^2=a\cdot c\) i taka też jest odpowiedź.

Teoria:      
W trakcie opracowania