W kartezjańskim układzie w współrzędnych \((x,y)\) przedstawiono fragmenty wykresów czterech funkcji: \(f, g, h, s\).





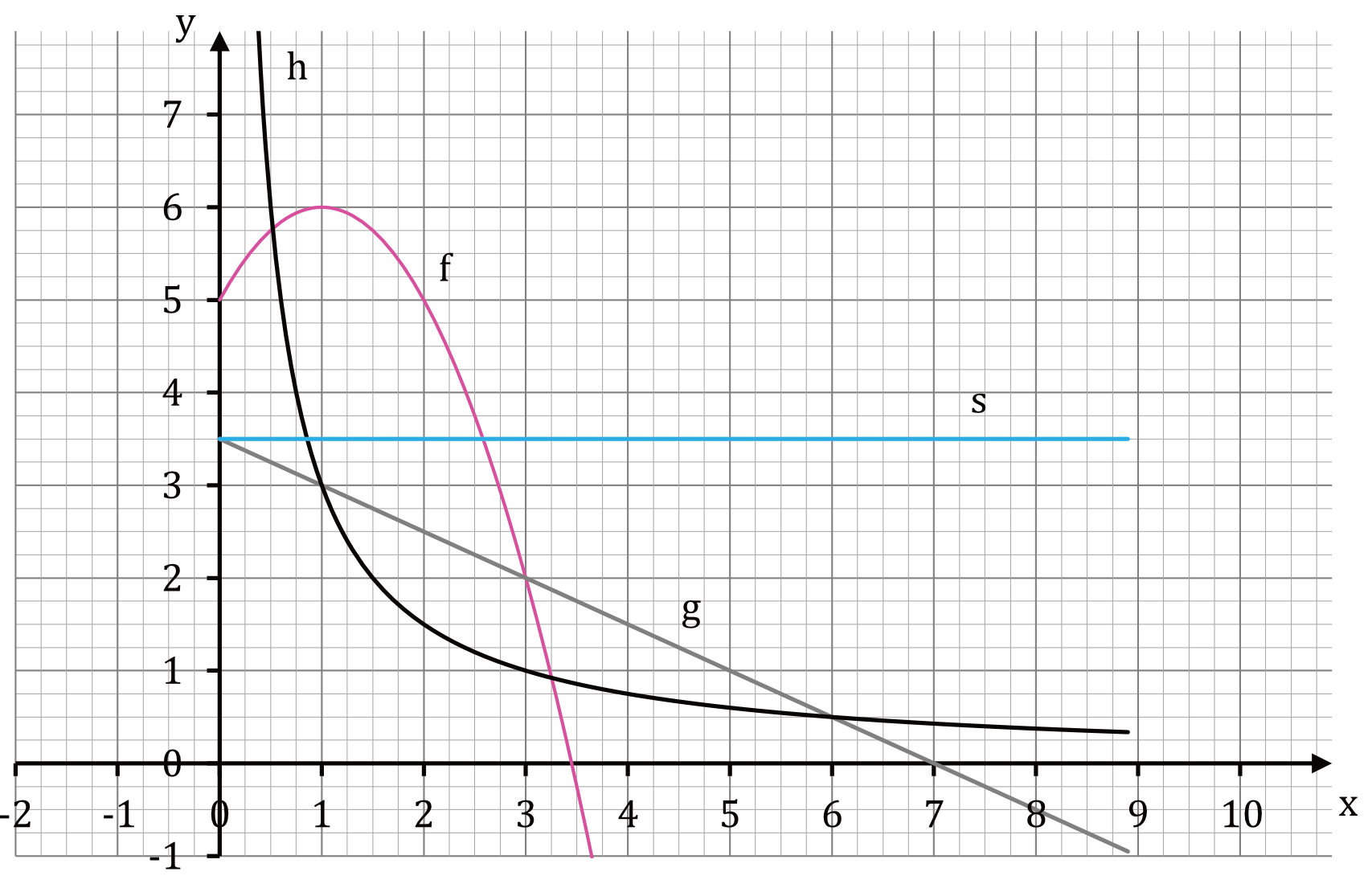
Zadanie 1.

Największą wartość dla argumentu \(x=2\) przyjmuje funkcja:

A. \(f\)

B. \(g\)

C. \(h\)

D. \(s\)



Zadanie 2. Dla argumentu \(x=3\) tę samą wartość przyjmują funkcje:

A. \(f\) i \(s\)

B. \(s\) i \(h\)

C. \(f\) i \(g\)

D. \(g\) i \(s\)



Zadanie 3. Zapisz maksymalny przedział, w którym prawdziwa jest nierówność \(g(x)\gt h(x)\).

Odpowiedź:      

1. A.
2. C.
3. \(x\in(1,6)\)

Rozwiązanie:      
Rozwiązanie 1. Przyglądając się wykresom funkcji, widzimy, że dla argumentu \(x=2\) najwyższą wartość osiągnie funkcja \(f\) (możemy nawet dodać, że ta wartość to \(y=5\)). Rozwiązanie 2. Jeśli dwie funkcje przyjmują tą samą wartość dla danego argumentu, to z praktycznego punktu widzenia, wykresy tych funkcji po prostu się przetną. Widzimy więc, że tą samą wartość dla argumentu \(x=3\) przyjmie funkcja \(f\) i \(g\). Rozwiązanie 3. Zgodnie z zapisem \(g(x)\gt h(x)\), interesuje nas sytuacja, w której dla danego argumentu, funkcja \(g(x)\) przyjmuje większe wartości niż \(h(x)\). Mówiąc bardziej obrazowo, musimy przeanalizować kiedy wykres funkcji \(g(x)\) znajduje się nad wykresem funkcji \(h(x)\). Widzimy, że taka sytuacja ma miejsce od argumentu \(x=1\) aż do \(x=6\), czyli interesującym nas przedziałem byłby \(x\in(1,6)\). Tak na marginesie - nawiasy dajemy otwarte, bo dla tych skrajnych argumentów obydwie funkcje przyjmują jednakową wartość, a nas interesuje sytuacja, w której wartości funkcji \(g\) są większe od funkcji \(h\).

Teoria:      
W trakcie opracowania