Z białych i szarych kwadratowych płytek ułożono mozaikę. Pierwsze dwa etapy jej powstawania pokazano na rysunku.





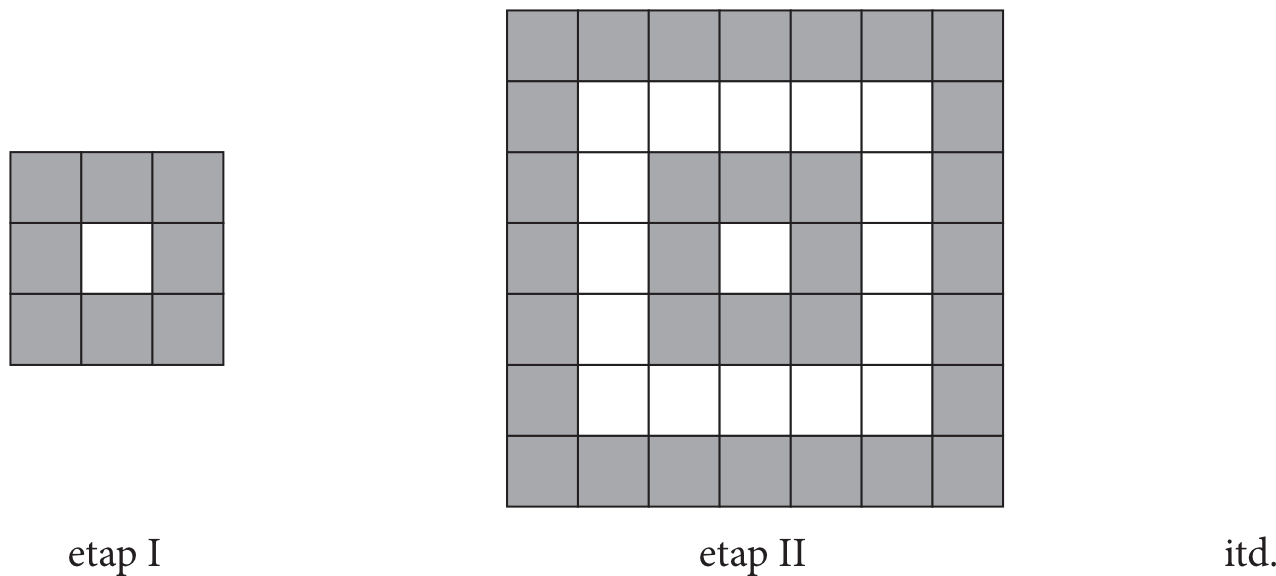
Ile szarych płytek dołożono na \(IV\) etapie tworzenia mozaiki?

A \(40\)
B \(48\)
C \(56\)
D \(64\)

Odpowiedź:      

C

Rozwiązanie:      
Kluczem do sukcesu jest dostrzeżenie prawidłowości, według której dokładane są szare płytki. Można do tego podejść na wiele różnych sposobów, więc jest tutaj spora dowolność. Najprościej będzie chyba zauważyć, że pierwszy etap ma wymiary \(3\times3\), drugi etap ma wymiary \(7\times7\), a każdy kolejny będzie miał o \(4\) płytki wzdłuż i wszerz więcej, czyli trzeci etap będzie miał \(11\times11\), a czwarty \(15\times15\). To teraz ustalmy ile szarych płytek zostanie dołożonych na tym czwartym etapie. Zostaną tam dołożone wszystkie te szare zewnętrzne płytki - czyli \(15\) płytek na dole, \(15\) na górze, \(15\) po lewej stronie i \(15\) po lewej. Licząc jednak w ten sposób, dublujemy płytki w narożnikach, więc te \(4\) zdublowane płytki musimy odjąć. To oznacza, że na \(IV\) etapie tworzenia mozaiki, liczba dołożonych płytek będzie równa: $$4\cdot15-4=60-4=56$$

Teoria:      
W trakcie opracowania