Na diagramie przedstawiono oceny z kartkówki z matematyki uzyskane przez uczniów klas 7a i 7b.





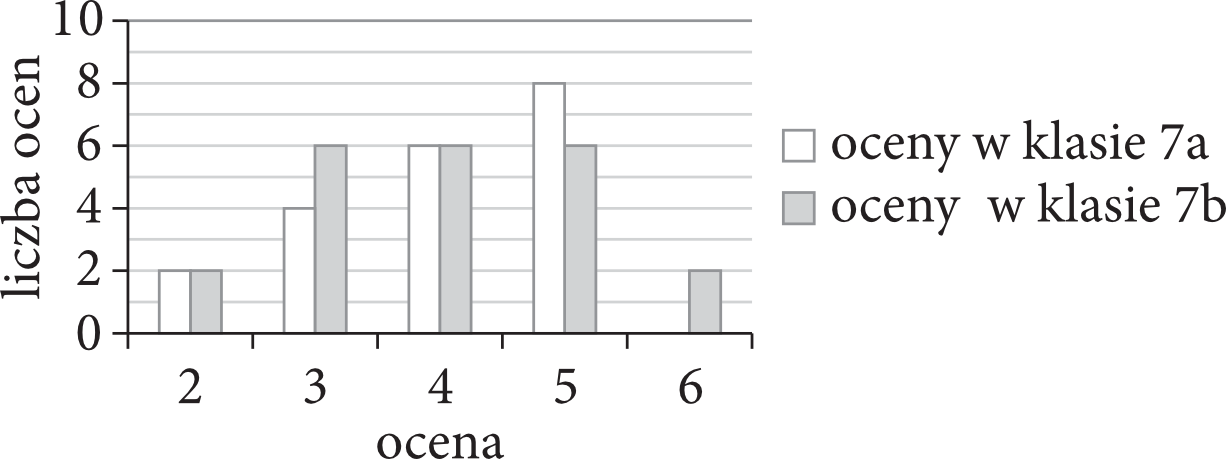
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. Średnia ocen z kartkówki w klasie 7a jest równa średniej ocen z tej kartkówki w klasie 7b.
Średnia ocen z kartkówki w obu klasach łącznie jest równa \(4\).

Średnia ocen z kartkówki w klasie 7a jest równa średniej ocen z tej kartkówki w klasie 7b.

Odpowiedź:      

1) PRAWDA

2) PRAWDA

Rozwiązanie:      
Krok 1. Obliczenie średniej arytmetycznej ocen. Policzmy średnią arytmetyczną ocen dla każdej z klas. Aby tego dokonać, musimy podzielić zdobyte oceny przez liczbę wszystkich uczniów, zatem: Klasa 7a: $$\frac{2\cdot2+4\cdot3+6\cdot4+8\cdot5+0\cdot6}{2+4+6+8+0}=\frac{4+12+24+40+0}{20}=\frac{80}{20}=4$$ Klasa 7b: $$\frac{2\cdot2+6\cdot3+6\cdot4+6\cdot5+2\cdot6}{2+6+6+6+2}=\frac{4+18+24+30+12}{22}=\frac{88}{22}=4$$ Krok 2. Ocena prawdziwości pierwszego zdania. Z obliczeń wykonanych w pierwszym kroku wynika, że to zdanie jest prawdą, bo faktycznie średnia ocen w obydwu klasach jest jednakowa. Krok 3. Ocena prawdziwości drugiego zdania. Drugie zdanie też jest prawdą, bo z obliczeń wyszło, że w obydwu klasach średnia ocen z kartkówki była równa \(4\).

Teoria:      
W trakcie opracowania