Na rysunku przedstawiono dwa czworokąty: trapez prostokątny i prostokąt. Długości boków tych figur opisano za pomocą wyrażeń algebraicznych (jak na rysunku).





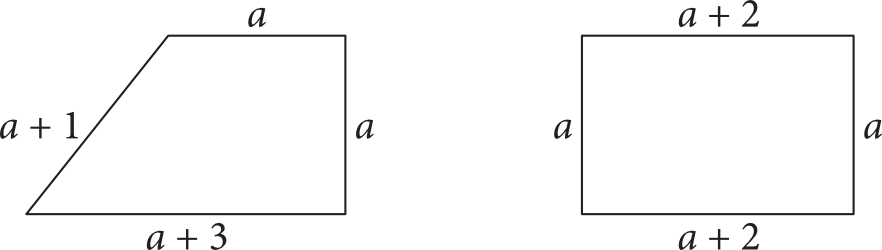
Które zdanie jest prawdziwe?

A Pole prostokąta jest mniejsze od pola trapezu.
B Pole prostokąta jest \(a\) razy większe od pola trapezu.
C Pole trapezu jest równe polu prostokąta.
D Pole trapezu jest o \(0,5a\) mniejsze od pola prostokąta.

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Obliczenie pola powierzchni trapezu. Zacznijmy od obliczenia pola powierzchni trapezu. Korzystając ze wzoru na pole tej figury, możemy zapisać, że: $$P_{t}=\frac{1}{2}(a+3+a)\cdot a \           ,\ P_{t}=\frac{1}{2}(2a+3)\cdot a \           ,\ P_{t}=\frac{1}{2}(2a^2+3a) \           ,\ P_{t}=a^2+1,5a$$ Krok 2. Obliczenie pola powierzchni prostokąta. Do rozwiązania zadania potrzebne nam jest jeszcze obliczenie pola prostokąta, zatem: $$P_{p}=(a+2)\cdot a \           ,\ P_{p}=a^2+2a$$ Krok 3. Wybór właściwej odpowiedzi. Przyglądając się otrzymanym wynikom widzimy, że jedynym prawdziwym zdaniem jest to ostatnie, czyli że pole trapezu jest o \(0,5a\) mniejsze od pola prostokąta, ponieważ: $$a^2+2a-(a^2+1,5a)=a^2+2a-a^2-1,5a=0,5a$$

Teoria:      
W trakcie opracowania