Dany jest sześcian \(ABCDEFGH\) o krawędzi długości \(a\). Punkty \(A, B, D\) i \(E\) są wierzchołkami ostrosłupa (zobacz rysunek).





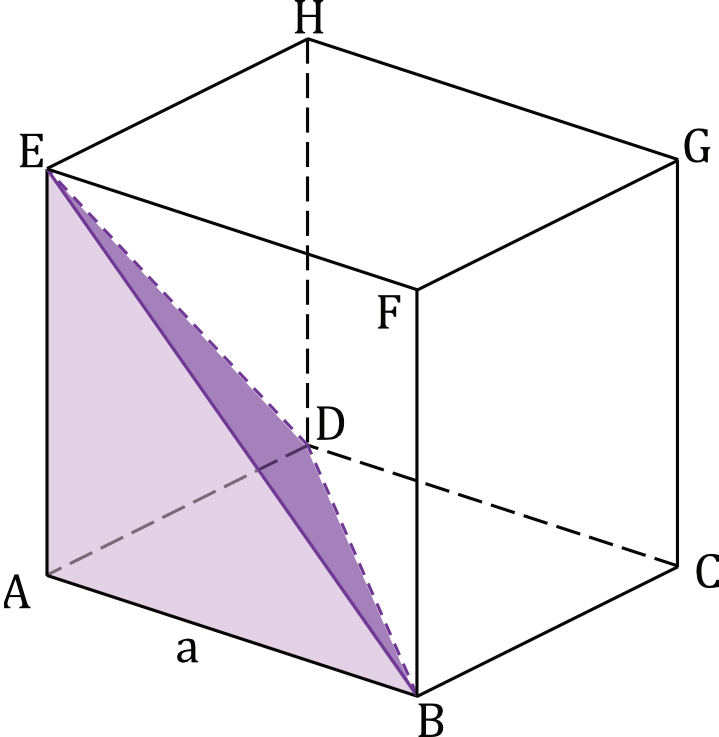
Oblicz pole powierzchni ostrosłupa \(ABDE\).

Odpowiedź:      

\(P_{c}=\frac{a^2\cdot(3+\sqrt{3})}{2}\)

Rozwiązanie:      
Krok 1. Obliczenie pól powierzchni poszczególnych ścian ostrosłupa. Na pole powierzchni całkowitej ostrosłupa \(ABDE\) składają się trzy trójkąty prostokątne \(ABD\), \(ABE\) oraz \(ADE\), a także trójkąt równoboczny \(BDE\). Obliczmy najpierw pole każdego z trójkątów prostokątnych. Trójkąty prostokątne mają przyprostokątne o długości \(a\), czyli ich pole powierzchni będzie równe: $$P_{ABD}=\frac{1}{2}\cdot a\cdot a \           ,\ P_{ABD}=\frac{1}{2}a^2$$ Trójkąt równoboczny ma bok o długości przekątnej podstawy. W podstawie sześcianu mamy oczywiście kwadrat, a z własności kwadratów wiemy, że kwadrat o boku \(a\) ma przekątną o długości \(a\sqrt{2}\). To oznacza, że nasz trójkąt równoboczny ma bok o długości \(a\sqrt{2}\). Korzystając zatem ze wzoru na pole trójkąta równobocznego możemy zapisać, że: $$P_{BDE}=\frac{(a\sqrt{2})^2\cdot\sqrt{3}}{4} \           ,\ P_{BDE}=\frac{a^2\cdot2\cdot\sqrt{3}}{4} \           ,\ P_{BDE}=\frac{a^2\sqrt{3}}{2}$$ Krok 2. Obliczenie pola powierzchni ostrosłupa. $$P_{c}=3\cdot\frac{1}{2}a^2+\frac{a^2\sqrt{3}}{2} \           ,\ P_{c}=\frac{3a^2}{2}+\frac{a^2\sqrt{3}}{2} \           ,\ P_{c}=\frac{3a^2+a^2\sqrt{3}}{2} \           ,\ P_{c}=\frac{a^2\cdot(3+\sqrt{3})}{2}$$

Teoria:      
W trakcie opracowania