Każda krawędź czworościanu \(ABCS\) ma długość \(a\). Punkty \(D\) i \(E\) są środkami boków – odpowiednio – \(AC\) oraz \(BC\) (zobacz rysunek).





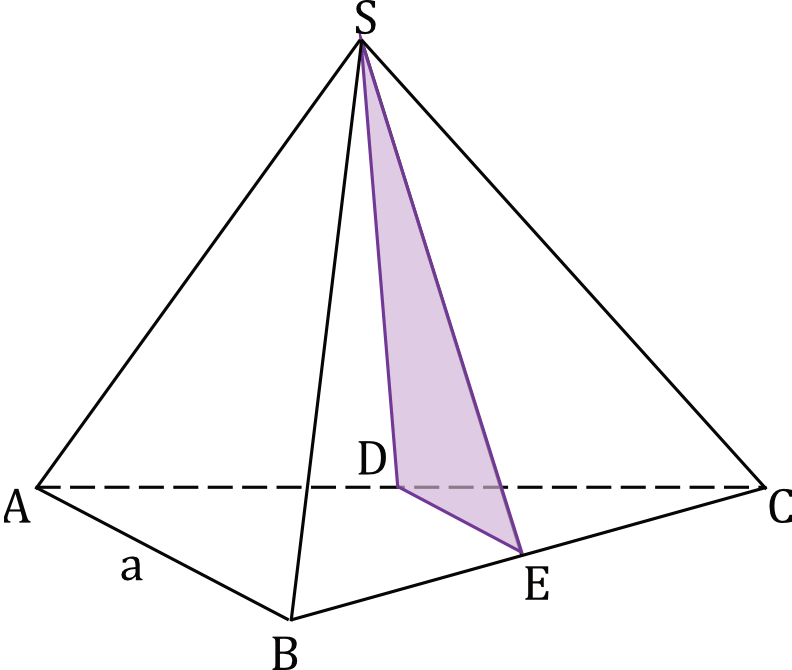
Oblicz pole trójkąta \(DES\).

Odpowiedź:      

\(P=\frac{a^2\sqrt{11}}{16}\)

Rozwiązanie:      
Krok 1. Wyznaczenie długości boków trójkąta \(DES\). Spójrzmy na trójkąt \(ECD\). Z treści zadania wynika, że będzie miał on ramiona \(EC\) oraz \(DC\) jednakowej długości, równej \(\frac{1}{2}a\). Dodatkowo wiemy, że kąt przy wierzchołku \(C\) ma miarę \(60°\). To prowadzi nas do wniosku, że jest to tak naprawdę trójkąt równoboczny, czyli tym samym \(|DE|=\frac{1}{2}a=\frac{a}{2}\). Boki \(DS\) oraz \(ES\) są wysokościami trójkątów równobocznych, które znalazły się w ścianach bocznych. Wysokość takich trójkątów opisujemy wzorem \(h=\frac{a\sqrt{3}}{2}\), stąd też możemy zapisać, że \(|DS|=\frac{a\sqrt{3}}{2}\) oraz \(|ES|=\frac{a\sqrt{3}}{2}\). Krok 2. Obliczenie pola powierzchni trójkąta \(DES\). W tym zadaniu skorzystamy z dość niecodziennego wzoru na pole trójkąta, który znajduje się w tablicach: $$P=\sqrt{p\cdot(p-a)\cdot(p-b)\cdot(p-c)}$$ Do tego wzoru musimy podstawić długości boków \(a\), \(b\) oraz \(c\), a także wartość \(p\), czyli połowę długości obwodu trójkąta. Obliczmy ją zatem oddzielnie: $$p=\frac{1}{2}\cdot\left(\frac{a}{2}+\frac{a\sqrt{3}}{2}+\frac{a\sqrt{3}}{2}\right) \           ,\ p=\frac{1}{2}\cdot\left(\frac{a+a\sqrt{3}+a\sqrt{3}}{2}\right) \           ,\ p=\frac{1}{2}\cdot\left(\frac{a+2a\sqrt{3}}{2}\right) \           ,\ p=\frac{a+2a\sqrt{3}}{4}$$ Teraz moglibyśmy od razu podstawić wszystkie znane dane do treści zadania, ale liczby są tutaj dość mocno rozbudowane, więc dość dobrym pomysłem byłoby obliczenie sobie osobno \(p-a\), \(p-b\) oraz \(p-c\), tak aby potem łatwiej było wykonywać obliczenia, zwłaszcza że trzeba tutaj sprowadzać liczby do wspólnego mianownika. W związku z tym: \(p-a=\frac{a+2a\sqrt{3}}{4}-\frac{a}{2}=\frac{a+2a\sqrt{3}}{4}-\frac{2a}{4}=\frac{2a\sqrt{3}-a}{4}\) \(p-b=\frac{a+2a\sqrt{3}}{4}-\frac{a\sqrt{3}}{2}=\frac{a+2a\sqrt{3}}{4}-\frac{2a\sqrt{3}}{4}=\frac{a}{4}\) \(p-c=\frac{a+2a\sqrt{3}}{4}-\frac{a\sqrt{3}}{2}=\frac{a+2a\sqrt{3}}{4}-\frac{2a\sqrt{3}}{4}=\frac{a}{4}\) Teraz podstawiając te różnice do wzoru na pole trójkąta, otrzymamy: $$P=\sqrt{\frac{a+2a\sqrt{3}}{4}\cdot\frac{2a\sqrt{3}-a}{4}\cdot\frac{a}{4}\cdot\frac{a}{4}}$$ Teraz dobrze byłoby zauważyć, ze przy mnożeniu dwóch pierwszych wyrażeń będziemy mogli zastosować wzór skróconego mnożenia \((a+b)(a-b)=a^2-b^2\). Całość moglibyśmy kontynuować w następujący sposób: $$P=\sqrt{\frac{2a\sqrt{3}+a}{4}\cdot\frac{2a\sqrt{3}-a}{4}\cdot\frac{a^2}{16}} \           ,\ P=\sqrt{\frac{4a^2\cdot3-a^2}{16}\cdot\frac{a^2}{16}} \           ,\ P=\sqrt{\frac{12a^2-a^2}{16}\cdot\frac{a^2}{16}} \           ,\ P=\sqrt{\frac{11a^2}{16}\cdot\frac{a^2}{16}} \           ,\ P=\frac{a\sqrt{11}}{4}\cdot\frac{a}{4} \           ,\ P=\frac{a^2\sqrt{11}}{16}$$

Teoria:      
W trakcie opracowania