W trójkącie równobocznym o boku długości \(a\) poprowadzono dwa odcinki równoległe do jednego z jego boków. Długości tych odcinków są równe \(b\) i \(c\), przy czym \(c\lt b\lt a\) (zobacz rysunek). Odcinki podzieliły trójkąt równoboczny na trzy figury: dwa trapezy i trójkąt.





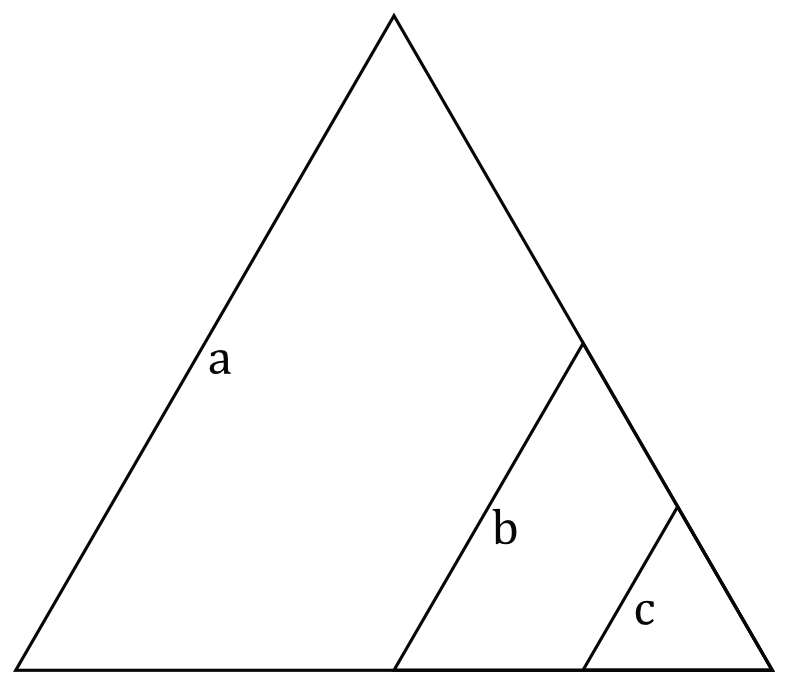
Wykaż, że stosunek pola trapezu o podstawach \(b\) i \(c\) do pola trapezu o podstawach \(a\) i \(b\) jest równy \(\dfrac{b^2-c^2}{a^2-b^2}\).

Odpowiedź:      

Udowodniono, rozpisując pola podanych trapezów.

Rozwiązanie:      
Krok 1. Zapisanie pól powierzchni trapezów. Wprowadźmy oznaczenia pól powierzchni dwóch trapezów jako \(P_{1}\) oraz \(P_{2}\), tak jak na rysunku: Pole \(P_{1}\) będzie różnicą między polem trójkąta równobocznego o boku \(a\) i pola trójkąta równobocznego o boku \(b\). Korzystając zatem ze wzoru na pole trójkąta równobocznego moglibyśmy zapisać, że: $$P_{1}=\frac{a^2\sqrt{3}}{4}-\frac{b^2\sqrt{3}}{4} \           ,\ P_{1}=\frac{a^2\sqrt{3}-b^2\sqrt{3}}{4} \           ,\ P_{1}=\frac{(a^2-b^2)\sqrt{3}}{4}$$ I analogicznie, pole trapezu \(P_{2}\) to różnica między polem trójkąta równobocznego o boku \(b\) i trójkąta równobocznego o boku \(c\), zatem: $$P_{2}=\frac{b^2\sqrt{3}}{4}-\frac{c^2\sqrt{3}}{4} \           ,\ P_{2}=\frac{b^2\sqrt{3}-c^2\sqrt{3}}{4} \           ,\ P_{2}=\frac{(b^2-c^2)\sqrt{3}}{4}$$ Krok 2. Obliczenie stosunku pól powierzchni. Celem zadania jest wyznaczenie stosunku pola powierzchni \(P_{2}\) względem \(P_{1}\), zatem: $$\frac{P_{2}}{P_{1}}=\frac{\frac{(b^2-c^2)\sqrt{3}}{4}}{\frac{(a^2-b^2)\sqrt{3}}{4}}=\frac{(b^2-c^2)\sqrt{3}}{4}\cdot\frac{4}{(a^2-b^2)\sqrt{3}}=\frac{b^2-c^2}{a^2-b^2}$$ Otrzymaliśmy dokładnie taką samą postać jak w treści zadania, zatem dowodzenie możemy uznać za zakończone.

Teoria:      
W trakcie opracowania