Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą \(2\) (zobacz rysunek).





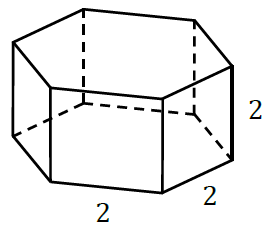
Pole powierzchni całkowitej tego graniastosłupa jest równe:

A \(24+2\sqrt{3}\)
B \(24+6\sqrt{3}\)
C \(24+12\sqrt{3}\)
D \(24+24\sqrt{3}\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Obliczenie pola powierzchni sześciokąta. Na początek obliczmy pole powierzchni sześciokąta, który znajduje się w dolnej i górnej podstawie naszej bryły. Z własności sześciokątów wynika, że jego pole będzie równe polu sześciu małych trójkątów równobocznych o boku \(2\), zatem: $$P_{p}=6\cdot\frac{a^2\sqrt{3}}{4} \           ,\ P_{p}=6\cdot\frac{2^2\sqrt{3}}{4} \           ,\ P_{p}=6\cdot\frac{4\sqrt{3}}{4} \           ,\ P_{p}=6\sqrt{3}$$ Krok 2. Obliczenie pola powierzchni całkowitej. Na pole powierzchni całkowitej składać się będą dwie podstawy (których pole policzyliśmy przed chwilą) oraz sześć kwadratowych ścian o boku \(2\). Skoro tak, to: $$P_{c}=2P_{p}+6P_{b} \           ,\ P_{c}=2\cdot6\sqrt{3}+6\cdot2\cdot2 \           ,\ P_{c}=12\sqrt{3}+24$$ To oznacza, że pole powierzchni całkowitej tego graniastosłupa jest równe \(24+12\sqrt{3}\).

Teoria:      
W trakcie opracowania