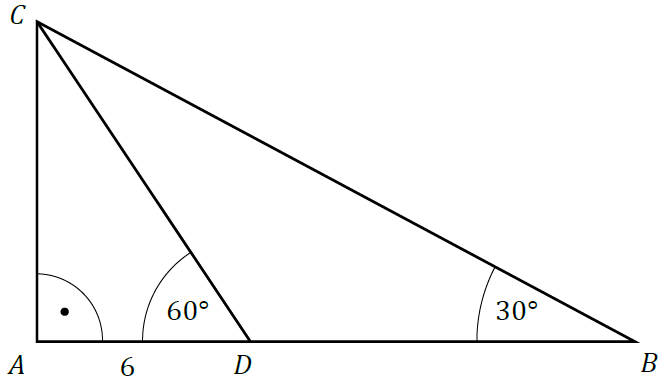
W trójkącie \(ABC\) kąt przy wierzchołku \(A\) jest prosty, a kąt przy wierzchołku \(B\) ma miarę \(30°\). Na boku \(AB\) tego trójkąta obrano punkt \(D\) tak, że miara kąta \(CDA\) jest równa \(60°\) oraz \(|AD|=6\) (zobacz rysunek). Oblicz \(|BD|\).

Odpowiedź:      

\(|BD|=12\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Wiedząc, że suma kątów w trójkącie jest równa \(180°\), powstanie nam następująca sytuacja: Kluczowym wnioskiem jaki płynie z tego rysunku jest to, że trójkąt \(DBC\) jest równoramienny, w którym \(|CD|=|BD|\). To obserwacja znacząco ułatwia rozwiązanie zadania, ponieważ długość odcinka \(CD\) jesteśmy w stanie podać niemalże od ręki, korzystając z własności trójkątów o kątach \(30°,60°,90°\). Krok 2. Obliczenie długości odcinka \(CD\) oraz \(BD\). Spójrzmy na trójkąt \(ADC\). Jest to trójkąt o kątach \(30°,60°,90°\). Z własności tych trójkątów wiemy, że przyprostokątna leżąca przy kącie \(60°\) jest dwa razy krótsza od przeciwprostokątnej, a to by oznaczało, że: $$|CD|=2\cdot6 \           ,\ |CD|=12$$ W pierwszym kroku ustaliliśmy już, że boki \(CD\) oraz poszukiwany \(BD\) mają jednakową miarę, zatem \(|BD|=12\).

Teoria:      
W trakcie opracowania