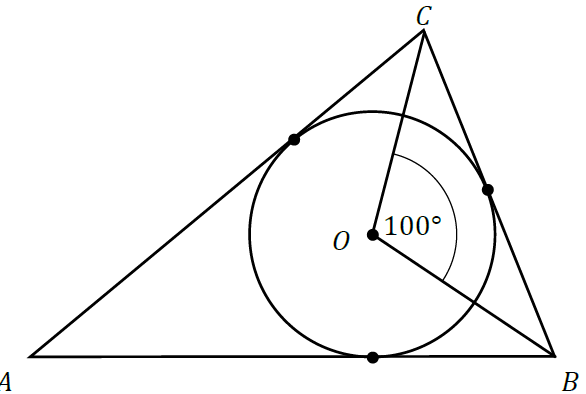Okrąg o środku w punkcie \(O\) jest wpisany w trójkąt \(ABC\). Wiadomo, że \(|AB|=|AC|\) i \(|\sphericalangle BOC|=100°\) (zobacz rysunek).





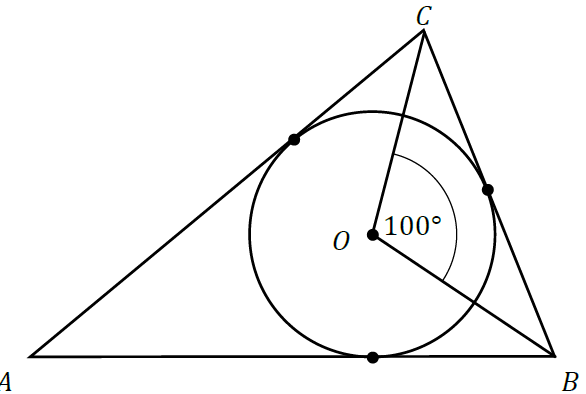
Miara kąta \(BAC\) jest równa:

A \(20°\)
B \(30°\)
C \(40°\)
D \(50°\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Obliczenie miar kątów \(OBC\) oraz \(OCB\). Spójrzmy na mały trójkąt COB. Jest to trójkąt równoramienny, zatem kąty przy podstawie BC będą mieć jednakową miarę. W tym trójkącie znamy już miarę jednego z kątów i jest to \(100°\), zatem na kąty \(OBC\) oraz \(OCB\) zostaje nam łącznie \(80°\). Skoro tak, to każdy z tych kątów ma po \(80°:2=40°\). Krok 2. Obliczenie miary kąta \(BAC\). Odcinki \(OB\) oraz \(OC\) są dwusiecznymi kątów \(ABC\) oraz \(ACB\). Skoro więc kąty \(OBC\) oraz \(OCB\) mają po \(40°\), to analogicznie kąty \(ABC\) oraz \(ACB\) mają po \(80°\). Suma kątów w trójkącie ABC musi być równa \(180°\), zatem: $$|\sphericalangle BAC|=180°-80°-80°=20°$$

Teoria:      
W trakcie opracowania