Punkty \(A\), \(B\), \(C\) i \(D\) leżą na okręgu o środku w punkcie \(O\). Cięciwy \(DB\) i \(AC\) przecinają się w punkcie \(E\), \(|\sphericalangle ACB|=55°\) oraz \(|\sphericalangle AEB|=140°\) (zobacz rysunek).





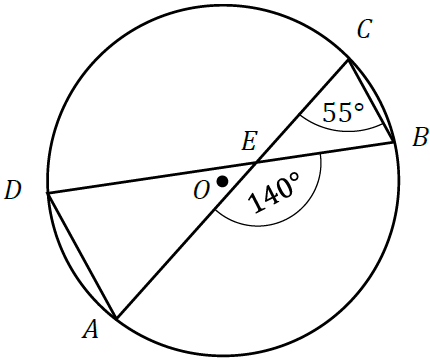
Miara kąta \(DAC\) jest równa:

A \(45°\)
B \(55°\)
C \(70°\)
D \(85°\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(CEB\). Kąt \(CEB\) jest kątem przyległym do znanego nam kąta \(AEB\) o mierze \(140°\). Suma kątów przyległych jest zawsze równa \(180°\), zatem: $$|\sphericalangle CEB|=180°-140°=40°$$ Krok 2. Obliczenie miary kąta \(EBC\). Spójrzmy na trójkąt \(EBC\). Znamy miary dwóch kątów w tym trójkącie, zatem miara trzeciego kąta, czyli kąta \(EBC\), będzie równa: $$|\sphericalangle EBC|=180°-40°-55°=85°$$ Krok 3. Obliczenie miary kąta \(DAC\). Powinniśmy dostrzec, że kąty \(EBC\) oraz \(DAC\) są kątami wpisanymi, które są oparte na tym samym łuku (na łuku \(DC\)). Skoro tak, to ich miara musi być jednakowa, zatem: $$|\sphericalangle DAC|=|\sphericalangle EBC|=85°$$

Teoria:      
W trakcie opracowania