Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura poprawkowa z matematyki (poziom podstawowy) - Sierpień 2021 Zadanie 12 z 35
Zadanie nr 12. (1pkt)
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \(f\).
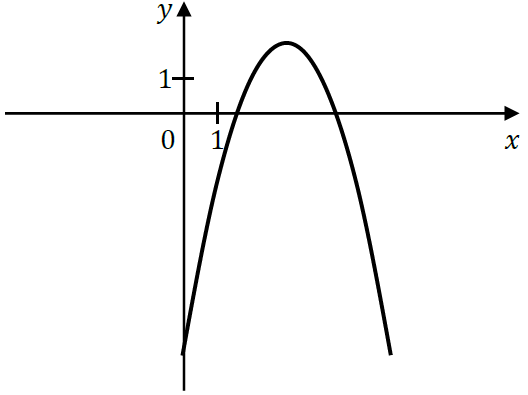
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji \(f\).
A \(f(x)=x^2-6x+11\)
B \(f(x)=-x^2+x+2\)
C \(f(x)=x^2-6x-7\)
D \(f(x)=-x^2+6x-7\)
Rozwiązanie:
Z wykresu wynika, że ramiona naszej paraboli są skierowane do dołu, a to oznacza, że współczynnik kierunkowy \(a\) musi być ujemny. Taką sytuację mamy jedynie w odpowiedzi B oraz D i tylko one będą już przez nas rozpatrywane.
Spójrzmy teraz na miejsce przecięcia się wykresu z osią \(OY\). Znajduje się ono pod osią \(OX\), a to oznacza, że współczynnik \(c\) musi być ujemny. Taką sytuację mamy właśnie w odpowiedzi D, zatem poszukiwanym wzorem funkcji będzie \(f(x)=-x^2+6x-7\).
Teoria:
W trakcie opracowania
matura poprawkowa - CKE

