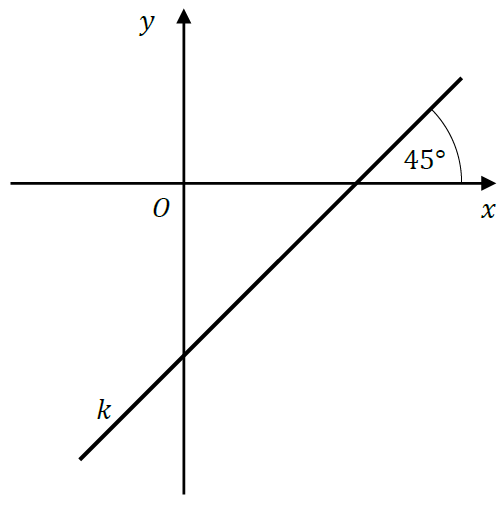
Prosta \(k\) przechodzi przez punkt \(A=(2,-3)\) i jest nachylona do osi \(Ox\) pod kątem \(45°\) (zobacz rysunek). Prosta \(k\) ma równanie:

A \(y=x-5\)
B \(y=-x-1\)
C \(y=-x+5\)
D \(y=x+5\)

Odpowiedź:      

A

Rozwiązanie:      
Do zadania możemy podejść na dwa sposoby: I sposób - analizując odpowiedzi. Widzimy, że wykres naszej funkcji jest rosnący, czyli tym samym współczynnik \(a\) musi być dodatni - taki znajduje się jedynie w odpowiedziach A oraz D. Dodatkowo wykres funkcji przecina oś \(OY\) dla ujemnych wartości igreka, a to oznacza, że współczynnik \(b\) będzie ujemny. To sprawia, że odpowiedź D musimy wykluczyć i tym samym zostaje nam odpowiedź A, czyli \(y=x-5\). II sposób - wyznaczając wzór samodzielnie. Wzór funkcji liniowej zapisujemy jako \(y=ax+b\). Chcąc samodzielnie wyznaczyć wzór tej funkcji (czyli poznać wartości współczynników \(a\) oraz \(b\)), musimy skorzystać z dość rzadko stosowanego wzoru, który mówi nam o tym, że współczynnik \(a=tg\alpha\), gdzie \(\alpha\) jest kątem jaki tworzą wykres funkcji z osią \(OX\). W naszym przypadku \(\alpha=45°\), zatem: $$a=tg45°$$ Z tablic trygonometrycznych możemy odczytać, że \(tg45°\) jest równy \(1\), zatem współczynnik \(a=1\). To oznacza, że naszą funkcję możemy zapisać jako \(y=1x+b\), czyli po prostu \(y=x+b\). Jak teraz poznać brakujący współczynnik \(b\)? Wiemy, że wykres przechodzi przez punkt o współrzędnych \((2,-3)\), zatem podstawiając \(x=2\) oraz \(y=-3\) do naszej wyznaczonej postaci \(y=x+b\), otrzymamy: $$-3=2+b \           ,\ b=-5$$ To oznacza, że nasza funkcja wyraża się wzorem \(y=x+(-5)\), czyli \(y=x-5\).

Teoria:      
W trakcie opracowania