W czworokącie \(ABCD\) o polu \(48cm^2\) przekątna \(AC\) ma długość \(8 cm\) i dzieli ten czworokąt na dwa trójkąty: \(ABC\) i \(ACD\) (zobacz rysunek). Wysokość trójkąta \(ACD\) poprowadzona z wierzchołka \(D\) do prostej \(AC\) jest równa \(2 cm\).





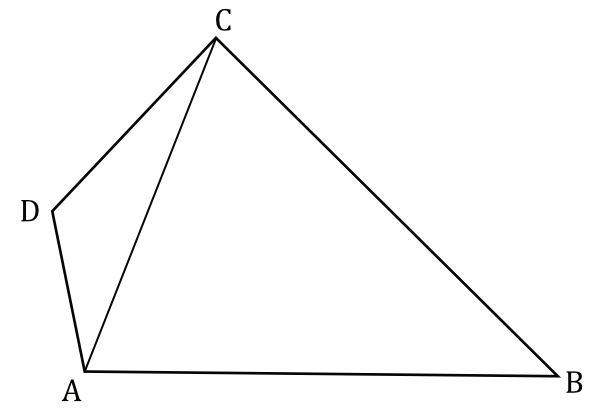
Oblicz wysokość trójkąta \(ABC\) poprowadzoną z wierzchołka \(B\) do prostej \(AC\). Zapisz obliczenia.

Odpowiedź:      

\(10cm\)

Rozwiązanie:      
Krok 1. Obliczenie pola powierzchni trójkąta \(ACD\). Z treści zadania wynika, że bok \(AC\) ma długośc \(8cm\), a wysokość opuszczona na ten bok ma długość \(2cm\). Skoro tak, to pole tego trójkąta jest równe: $$P=\frac{1}{2}\cdot a\cdot h \           ,\ P=\frac{1}{2}\cdot8cm\cdot2cm \           ,\ P=8cm^2$$ Krok 2. Obliczenie pola powierzchni trójkąta \(ABC\). Skoro cały czworokąt \(ABCD\) ma pole równe \(48cm^2\) i wiemy, że pole trójkąta \(ACD\) jest równe \(8cm^2\), to pole trójkąta \(ABC\) będzie równe: $$P_{ABC}=48cm^2-8cm^2 \           ,\ P_{ABC}=40cm^2$$ Krok 3. Obliczenie wysokości trójkąta \(ABC\) (opuszczonej z wierzchołka \(B\)). Wysokość z wierzchołka \(B\) pada na bok \(AC\), a wiemy, że ten bok ma długość \(8cm\) i tym samym będzie on podstawą naszego trójkąta. Skoro tak, to korzystając ze wzoru na pole trójkąta, zapisalibyśmy że: $$P=\frac{1}{2}\cdot a\cdot h \           ,\ 40cm^2=\frac{1}{2}\cdot8cm\cdot h \           ,\ 40cm^2=4cm\cdot h \           ,\ h=10cm$$

Teoria:      
W trakcie opracowania