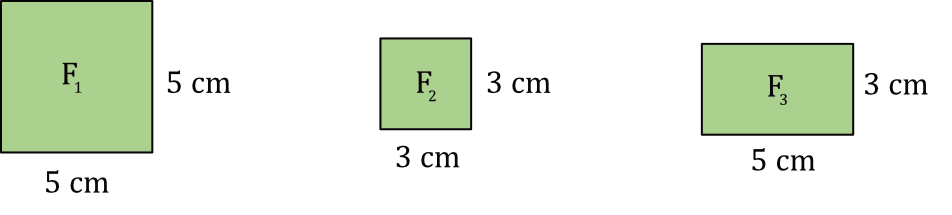Na rysunku przedstawiono trzy figury: kwadrat \(F_{1}\), kwadrat \(F_{2}\) i prostokąt \(F_{3}\), oraz podano ich wymiary.





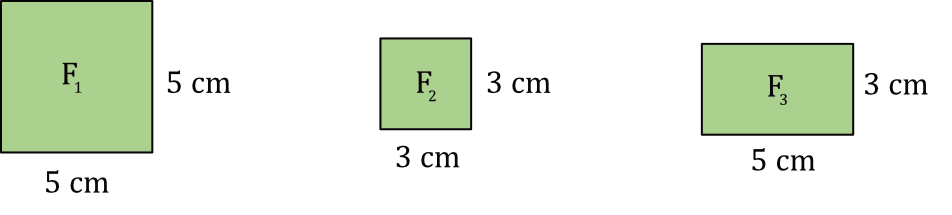
Czy z figur \(F_{1}, F_{2}, F_{3}\) można ułożyć, bez rozcinania tych figur, kwadrat \(K\) o polu \(49cm^2\)?



Wybierz odpowiedź A albo B i jej uzasadnienie spośród 1., 2. albo 3

Odpowiedź:      

Nie, ponieważ 3.

Rozwiązanie:      
Aby otrzymać kwadrat o polu \(49cm^2\) musielibyśmy mieć kwadrat o boku \(7cm\), ponieważ \(P=7cm\cdot7cm=49cm^2\). Podane w zadaniu figury mają boki o długościach \(3cm\) oraz \(5cm\), więc nie damy rady połączyć ich w taki sposób, by otrzymać kwadrat o boku \(7cm\), ponieważ zarówno \(3cm+3cm=6cm\) jak i \(3cm+5cm=8cm\). To oznacza, że prawidłową odpowiedzią będzie "Nie, ponieważ suma długości dowolnych boków figur \(F_{1}, F_{2}, F_{3}\) nie jest równa \(7cm\).

Teoria:      
W trakcie opracowania