W prostokącie \(ABCD\) punkty \(E\) i \(F\) są środkami boków \(BC\) i \(CD\) (zobacz rysunek). Długość odcinka \(EC\) jest równa \(6 cm\), a długość odcinka \(EF\) jest równa \(10 cm\).





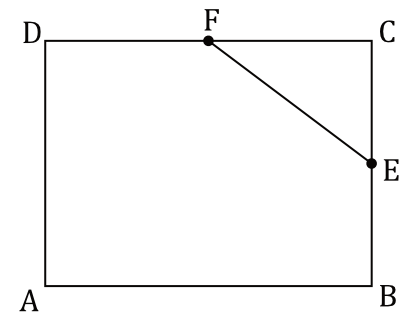
Obwód prostokąta \(ABCD\) jest równy:

A \(64 cm\)
B \(56 cm\)
C \(40 cm\)
D \(28 cm\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Obliczenie długości odcinka \(CF\). Spójrzmy na trójkąt \(ECF\). Jest to trójkąt prostokątny w którym przyprostokątna \(EC\) ma długość \(6cm\), natomiast przeciwprostokątna \(EF\) ma długość \(10cm\). Skoro tak, to korzystając z twierdzenia Pitagorasa moglibyśmy zapisać, że: $$|CF|^2+6^2=10^2 \           ,\ |CF|^2+36=100 \           ,\ |CF|^2=64 \           ,\ |CF|=8 \quad\lor\quad |CF|=-8$$ Ujemną długość oczywiście odrzucamy, bo bok ma dodatnią miarę, zatem zostaje nam \(|CF|=8\). Krok 2. Obliczenie długości boków prostokąta. Skoro punkty \(E\) i \(F\) są środkami boków \(BC\) i \(CD\), to odcinek \(EC\) jest połową boku krótszego boku prostokąta \(BC\) i analogicznie odcinek \(CF\) jest połową dłuższego boku \(CD\). Skoro tak, to krótszy bok prostokąta ma długość \(|BC|=2\cdot6cm=12cm\), natomiast dłuższy bok prostokąta ma długość \(|CD|=2\cdot8cm=16cm\). Krok 3. Obliczenie obwodu prostokąta. Obwód prostokąta będzie zatem równy: $$Obw=2\cdot12cm+2\cdot16cm \           ,\ Obw=24cm+32cm \           ,\ Obw=56cm$$

Teoria:      
W trakcie opracowania