Przyprostokątna \(AC\) trójkąta prostokątnego \(ABC\) ma długość \(8\) oraz \(tg\alpha=\frac{2}{5}\) (zobacz rysunek).





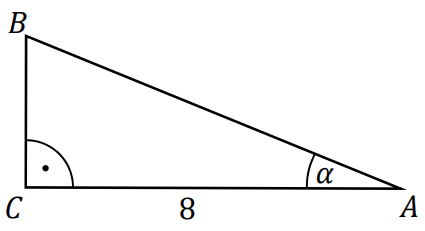
Pole tego trójkąta jest równe:

A \(12\)
B \(\frac{37}{3}\)
C \(\frac{62}{5}\)
D \(\frac{64}{5}\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Obliczenie wysokości trójkąta. Tangens opisuje stosunek długości przyprostokątnej leżącej naprzeciwko kąta \(\alpha\) względem przyprostokątnej leżącej przy tym kącie. Skoro tak, to możemy zapisać, że: $$tg\alpha=\frac{|BC|}{|CA|}$$ Podstawiając dane z treści zadania otrzymamy: $$\frac{2}{5}=\frac{|BC|}{8} \           ,\ |BC|=\frac{16}{5}$$ Odcinek |BC| jest jednocześnie wysokością naszego trójkąta, zatem \(h=\frac{16}{5}\). Krok 2. Obliczenie pola powierzchni trójkąta. Korzystając ze standardowego wzoru na pole trójkąta, możemy zapisać, że: $$P=\frac{1}{2}ah \           ,\ P=\frac{1}{2}\cdot8\cdot\frac{16}{5} \           ,\ P=\frac{64}{5}$$

Teoria:      
W trakcie opracowania