Na rysunku obok przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań. Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.

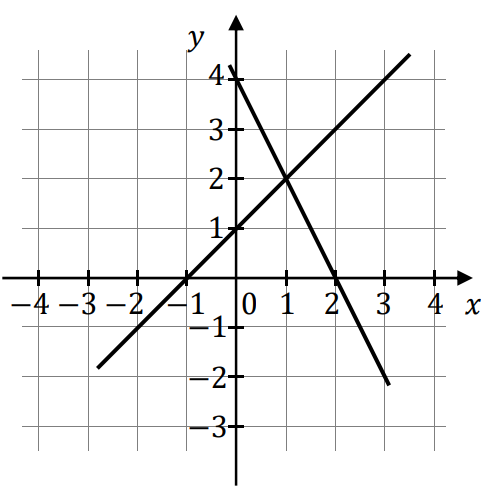
A \(\begin{cases}y=x+1 \\ y=-2x+4\end{cases}\)
B \(\begin{cases}y=x-1 \\ y=2x+4\end{cases}\)
C \(\begin{cases}y=x-1 \\ y=-2x+4\end{cases}\)
D \(\begin{cases}y=x+1 \\ y=2x+4\end{cases}\)

Odpowiedź:      

A

Rozwiązanie:      
Do zadania da się podejść na kilka sposobów. Z geometrycznej interpretacji wiemy, że rozwiązaniem układu równań są współrzędne punktu przecięcia się tych dwóch prostych. Możemy oczywiście rozwiązać każdy układ i sprawdzić kiedy otrzymamy wynik \(x=1\) oraz \(y=2\) (bo z rysunku wynika, że właśnie w tym miejscu te dwie proste się przecinają). Możemy też postąpić nieco sprytniej i wręcz podstawić \(x=1\) oraz \(y=2\) do każdego układu. Obydwie te metody są dobre, choć czasochłonne (a i czasem możemy wpaść w pułapkę związaną z tym, że pasować będą dwa układy równań). Najlepiej byłoby dostrzec, że jedna prosta jest rosnąca, a druga malejąca - czyli jedna prosta musi mieć dodatni współczynnik kierunkowy \(a\), natomiast druga musi mieć ten współczynnik ujemny. Pasują nam już zatem tylko odpowiedzi A oraz C. Teraz spójrzmy na miejsce przecięcia się prostych z osią \(OY\). Prosta rosnąca przecina oś \(OY\) dla \(y=1\), więc współczynnik \(b\) tej prostej musi być równy \(b=1\). Analogicznie prosta malejąca przecina oś \(OY\) dla \(y=4\), więc \(b=4\). To oznacza, że pasuje nam już tylko odpowiedź A.

Teoria:      
W trakcie opracowania