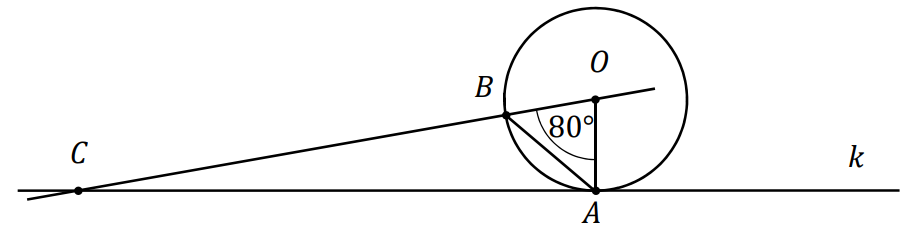
Prosta \(k\) jest styczna w punktach \(A\) do okręgu o środku \(O\). Punkt \(B\) leży na tym okręgu i miara kąta \(AOB\) jest równa \(80\) stopni. Przez punkty \(O\) i \(B\) poprowadzono prostą \(k\) w punkcie \(C\) (zobacz rysunek). Miara kąta \(BAC\) jest równa:

A \(10°\)
B \(30°\)
C \(40°\)
D \(50°\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(BAO\). Spójrzmy na trójkąt \(AOB\). Na pewno jest to trójkąt równoramienny, bowiem boki \(AO\) oraz \(BO\) są promieniami okręgu. Skoro tak, to kąty przy podstawie \(AB\) muszą mieć jednakową miarę. Jeżeli więc kąt między ramionami ma miarę \(80°\), to na kąty przy podstawie zostaje: $$180°-80°=100°$$ Obydwa kąty muszą mieć jednakową miarę, zatem: $$|\sphericalangle BAO|=100°:2=50°$$ Krok 2. Wyznaczenie miary kąta \(BAC\). Spójrzmy na trójkąt \(CAO\). Jest to trójkąt prostokątny, bo styczna do okręgu zawsze tworzy z promieniem kąt prosty. Poszukiwany kąt \(BAC\) będzie więc różnicą między kątem prostym i kątem \(BAO\) (który przed chwilą wyznaczyliśmy). W związku z tym: $$|\sphericalangle BAC|=90°-50°=40°$$

Teoria:      
W trakcie opracowania