Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura próbna z matematyki (poziom podstawowy) - Listopad 2009 Zadanie 18 z 34
Zadanie nr 18. (1pkt)
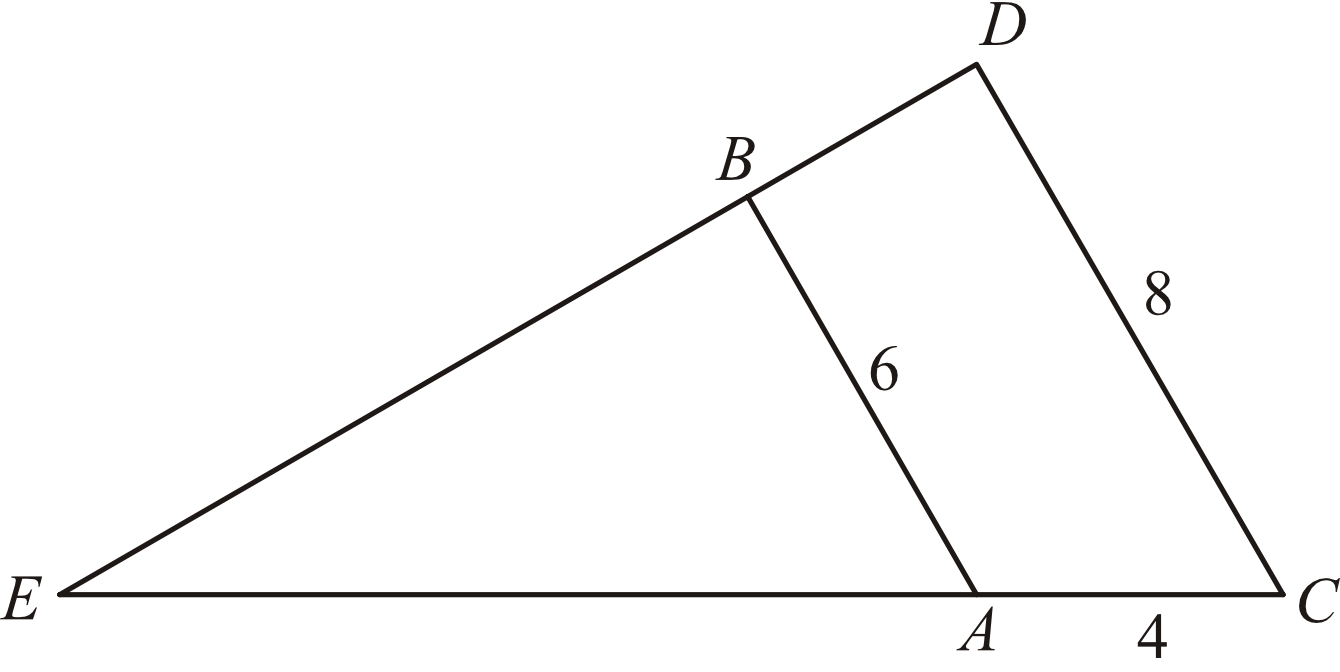
Oblicz długość odcinka \(AE\) wiedząc, że \(AB||CD\) i \(|AB|=6\), \(|AC|=4\), \(|CD|=8\).
A \(|AE|=2\)
B \(|AE|=4\)
C \(|AE|=6\)
D \(|AE|=12\)
Rozwiązanie:
Krok 1. Zbudowanie równania na podstawie danych z treści zadania.
Wiedząc, że proste \(AB\) oraz \(CD\) są równoległe możemy stwierdzić, że trójkąty \(EAB\) oraz \(ECD\) są trójkątami podobnymi. W związku z tym prawdziwa będzie relacja:
$$\frac{|EA|}{|AB|}=\frac{|EC|}{|CD|} \ ,\
\frac{x}{6}=\frac{x+4}{8}$$
Zwróć szczególną uwagę na odcinek \(EC\). Bardzo często w tego typu zadaniach uczniowie wpisują w tym miejscu długość odcinka \(AC\), co jest błędem.
Krok 2. Rozwiązanie powstałego równania.
Najprościej będzie wykonać mnożenie na krzyż, zatem:
$$8x=6\cdot(x+4) \ ,\
8x=6x+24 \ ,\
2x=24 \ ,\
x=12$$
Długość odcinka \(|AE|\) oznaczono na rysunku jako \(x\), więc \(|AE|=12\).
Teoria:
W trakcie opracowania
matura próbna - CKE

