Prostokąt \(ABCD\) podzielono na \(6\) kwadratów: jeden duży, dwa średnie i trzy małe, jak na rysunku.





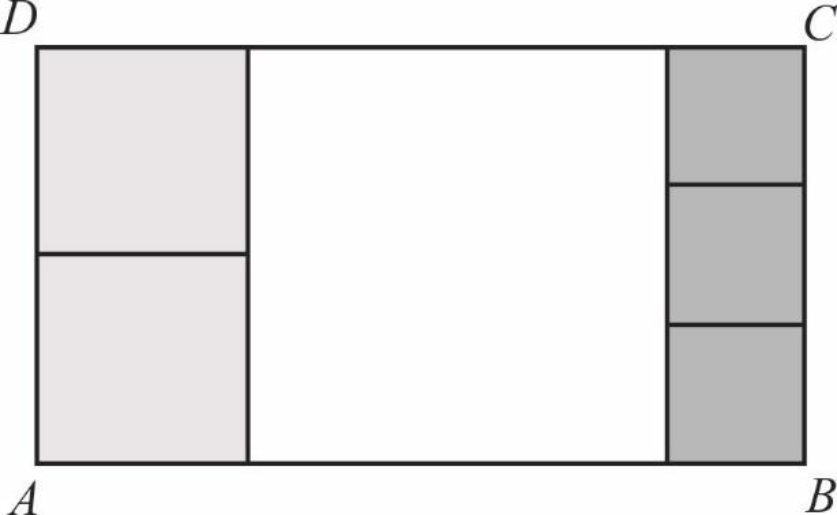
Uzasadnij, że pole powierzchni dużego kwadratu jest większe niż połowa powierzchni prostokąta \(ABCD\).

Odpowiedź:      

Udowodniono obliczając pola poszczególnych figur.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Oznaczmy sobie długość boku małego kwadratu jako \(x\). To będzie oznaczać, że duży kwadrat będzie mieć długość \(3x\), a średni kwadrat będzie mieć bok długości \(1,5x\): Krok 2. Obliczenie pola prostokąta \(ABCD\). Zgodnie z rysunkiem możemy powiedzieć, że nasz prostokąt ma boki długości \(5,5x\) oraz \(3x\), zatem jego pole powierzchni będzie równe: $$P=5,5x\cdot3x \           ,\ P=16,5x^2$$ Krok 3. Obliczenie pola dużego kwadratu. Duży kwadrat ma bok długości \(3x\), zatem jego pole powierzchni będzie równe: $$P=3x\cdot3x \           ,\ P=9x^2$$ Krok 4. Zakończenie dowodzenia. Duży kwadrat ma pole równe \(9x^2\). Połowa pola prostokąta \(ABCD\) wynosi \(16,5x^2:2=8,25x^2\). To oznacza, że pole dużego kwadratu jest rzeczywiście większe niż połowa prostokąta \(ABCD\).

Teoria:      
W trakcie opracowania