Bok \(CD\) kwadratu \(ABCD\) podzielono punktami \(E\) i \(F\) na trzy odcinki równej długości. Przez wierzchołek \(A\) kwadratu i przez punkt \(E\) poprowadzono prostą. Pole trójkąta \(AED\) wynosi \(24cm^2\).





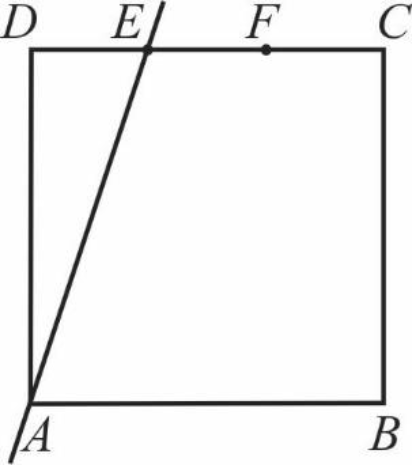
Oblicz pole kwadratu \(ABCD\).

Odpowiedź:      

Pole kwadratu wynosi \(144cm^2\).

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Jeżeli założymy sobie, że kwadrat ma bok długości \(a\), to zgodnie z treścią zadania odcinek \(DE\) ma długość \(\frac{1}{3}a\). Krok 2. Obliczenie długości boku kwadratu. Wiemy że trójkąt \(AED\) jest trójkątem prostokątnym i ma pole równe \(24cm^2\). Podstawa tego trójkąta ma długość \(\frac{1}{3}a\), natomiast wysokość ma długość \(a\). Wykorzystując więc wzór na pole trójkąta możemy ułożyć równanie z którego obliczymy długość boku \(a\) (czyli tym samym długość boku kwadratu). $$\frac{1}{2}\cdot\frac{1}{3}a\cdot a=24 \           ,\ \frac{1}{6}a^2=24 \           ,\ a^2=144 \           ,\ a=12[cm]$$ Krok 3. Obliczenie pola kwadratu. Wiemy już, że nasz kwadrat ma bok długości \(12cm\), zatem jego pole będzie równe: $$P=12cm\cdot12cm \           ,\ P=144cm^2$$

Teoria:      
W trakcie opracowania