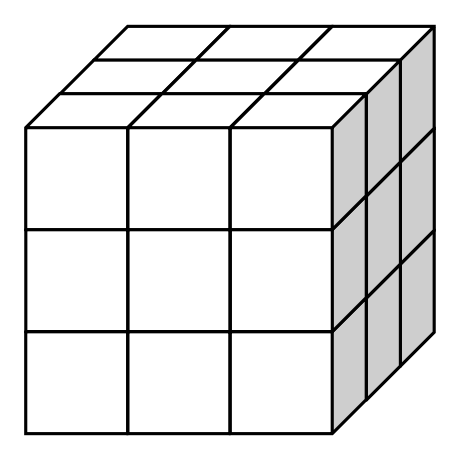
Drewnianą kostkę sześcienną o krawędzi długości \(30cm\) rozcięto na \(27\) jednakowych mniejszych sześciennych kostek. Z ośmiu takich małych kostek ułożono nowy sześcian.





Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. Pole powierzchni nowego sześcianu jest równe \(4800cm^2\).
Objętość nowego sześcianu jest równa \(8000cm^3\).

Pole powierzchni nowego sześcianu jest równe \(4800cm^2\).

Odpowiedź:      

1) FAŁSZ

2) PRAWDA

Rozwiązanie:      
Krok 1. Obliczenie długości krawędzi pojedynczej kostki. Skoro sześcian o krawędzi długości \(30cm\) podzielono dokładnie tak jak przedstawia to rysunek, to każda mała kostka ma wymiary \(10cm\times10cm\times10cm\). Krok 2. Ocena prawdziwości pierwszego zdania. Z ośmiu kostek możemy złożyć następujący sześcian: Widzimy więc, że jest to sześcian o boku \(20cm\). To oznacza, że jego pole powierzchni będzie równe: $$P_{c}=6a^2 \           ,\ P_{c}=6\cdot20^2 \           ,\ P_{c}=6\cdot400 \           ,\ P_{c}=2400[cm^2]$$ Pierwsze zdanie jest więc nieprawdą. Krok 3. Ocena prawdziwości drugiego zdania. Korzystamy z tego samego sześcianu co w kroku drugim. Jego objętość będzie równa: $$V=a^3 \           ,\ V=20^3 \           ,\ V=8000[cm^3]$$ Drugie zdanie jest więc prawdą.

Teoria:      
W trakcie opracowania