W okręgu o środku \(S\) zaznaczono kąt oparty na łuku \(AB\). Przez punkt \(B\) poprowadzono prostą \(k\) styczną do okręgu.





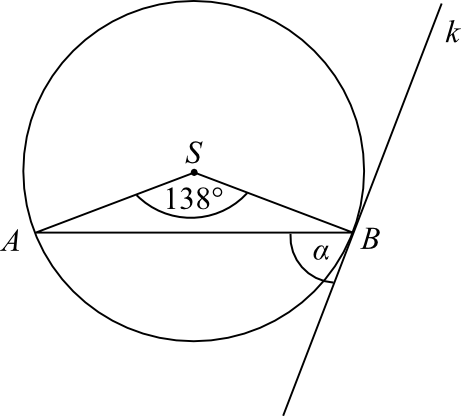
Zaznaczony na rysunku kąt \(α\) zawarty między styczną \(k\) i cięciwą \(AB\) ma miarę:

A \(21°\)
B \(42°\)
C \(48°\)
D \(69°\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Ustalenie miar kątów ostrych w trójkącie \(ABS\). Nasz trójkąt wpisany w okrąg jest na pewno trójkątem równoramiennym (ramiona mają jednakową długość równą długości promienia okręgu), a to z kolei oznacza, że kąty przy podstawie tego trójkąta mają jednakową miarę. Skoro suma kątów w trójkącie wynosi 180°, to każdy z kątów ostrych musi mieć: $$(180°-138°):2=42°:2=21°$$ Krok 2. Obliczenie miary kąta \(α\). Musimy wiedzieć, że styczna do okręgu jest zawsze prostopadła względem promienia okręgu. To znaczy, że kąt \(α\) wraz z kątem ostrym \(ABS\) tworzy kąt \(90°\). Jeżeli kąt \(ABS\) ma miarę \(21°\), to poszukiwany kąt ma miarę: $$α=90°-21°=69°$$

Teoria:      
W trakcie opracowania