Na rysunku przedstawiono sposób ułożenia wzoru z jednakowych elementów i podano długości dwóch fragmentów tego wzoru.





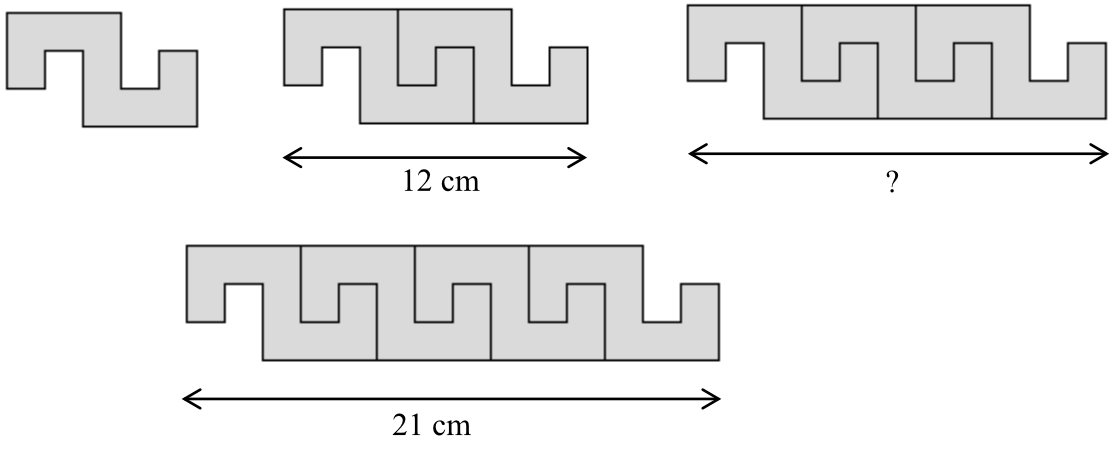
Fragment wzoru złożony z \(3\) elementów ma długość:

A \(15cm\)
B \(15,75cm\)
C \(16,5cm\)
D \(18cm\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Interpretacja rysunku. Musimy dobrze zinterpretować rysunek. Na pewno nie można wnioskować, że skoro \(2\) elementy zajmują \(12cm\), to \(1\) element zajmuje \(6cm\), zatem \(3\) elementy zajmą \(18cm\). Ten wniosek byłby błędny, bo elementy zachodzą na siebie. Trzeba więc zauważyć, że jak do jednego elementu startowego dołożyliśmy jeden puzzel to długość figury wynosi \(12cm\). Jak do elementu startowego dołożyliśmy trzy puzzle, to długość wzrosła do \(21cm\). Krok 2. Ułożenie i rozwiązanie układu równań. Matematycznie zapisując nasze wnioski z pierwszego kroku otrzymamy: \(x\) - puzzel startowy \(y\) - puzzle dołożone $$\begin{cases} x+y=12 \           ,\ x+3y=21 \end{cases}$$ Przekształcając pierwsze równanie do postaci \(x=12-y\) możemy zastosować metodę podstawiania: $$12-y+3y=21 \           ,\ 12+2y=21 \           ,\ 2y=9 \           ,\ y=4,5$$ Podstawiając obliczonego igreka np. do pierwszego równania otrzymamy: $$x+4,5=12 \           ,\ x=7,5$$ To oznacza, że puzzel startowy zajmuje \(7,5cm\), a każdy kolejny dołożony powiększa długość figury o \(4,5cm\). Krok 3. Obliczenie długości poszukiwanej figury. Nas interesuje długość figury składającej się z jednego elementu podstawowego oraz dwóch elementów dodanych, zatem: $$x+2y=7,5+2\cdot4,5=7,5+9=16,5[cm]$$

Teoria:      
W trakcie opracowania