Z kartki w kształcie kwadratu o boku \(6\) odcięto ćwierć koła o promieniu \(6\) (patrz rysunek).





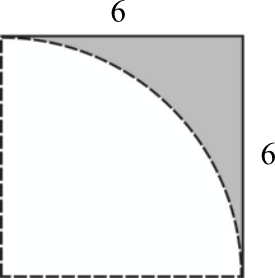
Pole powierzchni pozostałej zacieniowanej części kartki jest równe:

A \(144-12π\)
B \(144-36π\)
C \(36-3π\)
D \(36-9π\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Obliczenie pola kwadratu. Na samym początku musimy obliczyć pole kwadratu z którego wycięto fragment koła. Pole to będzie równe: $$P_{kw}=6\cdot6=36$$ Krok 2. Obliczenie pola ćwiartki koła. Wzór na pole koła jest następujący: $$P_{k}=πr^2$$ My potrzebujemy znać pole ćwiartki koła, więc postawimy na początku wzoru mnożenie przez \(\frac{1}{4}\). Promień koła jest równy \(6\), zatem: $$P_{ćw}=\frac{1}{4}πr^2 \           ,\ P_{ćw}=\frac{1}{4}π\cdot6^2 \           ,\ P_{ćw}=\frac{1}{4}π\cdot36 \           ,\ P_{ćw}=9π$$ Krok 3. Obliczenie pola zacieniowanej części kartki. Nasza zacieniowana część będzie mieć powierzchnię równą różnicy między polem kwadratu, a polem ćwiartki: $$P_{z}=P_{k}-P_{ćw} \           ,\ P_{z}=36-9π$$

Teoria:      
W trakcie opracowania