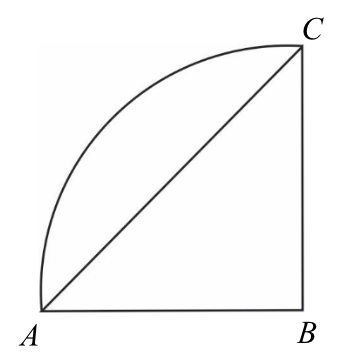
Pole ćwiartki koła przedstawionej na rysunku jest równe \(4π cm^2\). Pole trójkąta \(ABC\) jest równe:

A \(4cm^2\)
B \(8cm^2\)
C \(16cm^2\)
D \(32cm^2\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Obliczenie pola powierzchni całego koła. Skoro ćwiartka koła ma pole równe \(4πcm^2\), to całe koło ma pole powierzchni równe: $$P=4\cdot4π cm^2 \           ,\ P=16π cm^2$$ Krok 2. Obliczenie długości boków \(AB\) oraz \(BC\). Boki \(AB\) oraz \(BC\) to tak naprawdę długość promienia koła, którego pole przed chwilą policzyliśmy: W związku z tym obliczając długość promienia koła poznamy długości kluczowych boków tego trójkąta. Długość promienia obliczymy korzystając ze wzoru na pole koła: $$P=πr^2 \           ,\ 16πcm^2=πr^2 \           ,\ r^2=16cm^2 \           ,\ r=4cm$$ Krok 3. Obliczenie pola trójkąta \(ABC\). Skoro boki \(AB\) oraz \(BC\) mają długość \(4cm\), to pole tego trójkąta będzie równe: $$P=\frac{1}{2}\cdot4cm\cdot4cm \           ,\ P=8cm^2$$

Teoria:      
W trakcie opracowania