W układzie współrzędnych zaznaczono trzy punkty \(A, B, C\) o współrzędnych całkowitych, jak na rysunku.





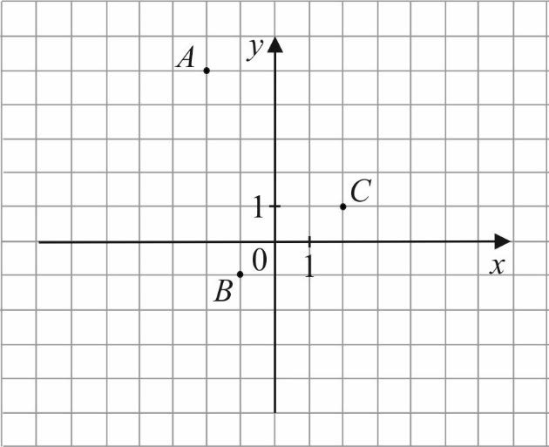
Które z tych punktów należą do wykresu funkcji określonej wzorem \(y=2x^2-3\)?

A \(A\), \(B\) i \(C\)
B Tylko \(A\) i \(C\)
C Tylko \(B\) i \(C\)
D Tylko \(A\) i \(B\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Odczytanie współrzędnych punktów. Aby rozwiązać to zadanie musimy najpierw odczytać współrzędne poszczególnych punktów, które to potem podstawimy do wzoru funkcji: $$A=(-2;5) \           ,\ B=(-1;-1) \           ,\ C=(2;1)$$ Krok 2. Sprawdzenie, czy dany punkt należy do funkcji. Dany punkt będzie należał do wykresu funkcji, jeśli po podstawieniu współrzędnej iksowej oraz igrekowej, lewa i prawa strona równania będą sobie równe. Punkt \(A\): \(x=-2\) oraz \(y=5\) \(y=2x^2-3 \           ,\ 5=2\cdot(-2)^2-3 \           ,\ 5=2\cdot4-3 \           ,\ 5=8-3 \           ,\ 5=5 \           ,\ L=P\) Punkt \(B\): \(x=-1\) oraz \(y=-1\) \(y=2x^2-3 \           ,\ -1=2\cdot(-1)^2-3 \           ,\ -1=2\cdot1-3 \           ,\ -1=2-3 \           ,\ -1=-1 \           ,\ L=P\) Punkt \(C\): \(x=2\) oraz \(y=1\) \(y=2x^2-3 \           ,\ 1=2\cdot2^2-3 \           ,\ 1=2\cdot4-3 \           ,\ 1=8-3 \           ,\ 1=5 \           ,\ L\neq P\) Lewa i prawa strona są sobie równe jedynie w przypadku podstawienia współrzędnych punktu \(A\) oraz \(B\), zatem tylko te punkty należą do wykresu naszej funkcji.

Teoria:      
W trakcie opracowania