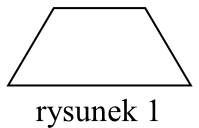
W ośrodku szkoleniowym są jednakowe stoliki, których blaty mają kształt trapezów równoramiennych, jak przedstawiono na rysunku 1.





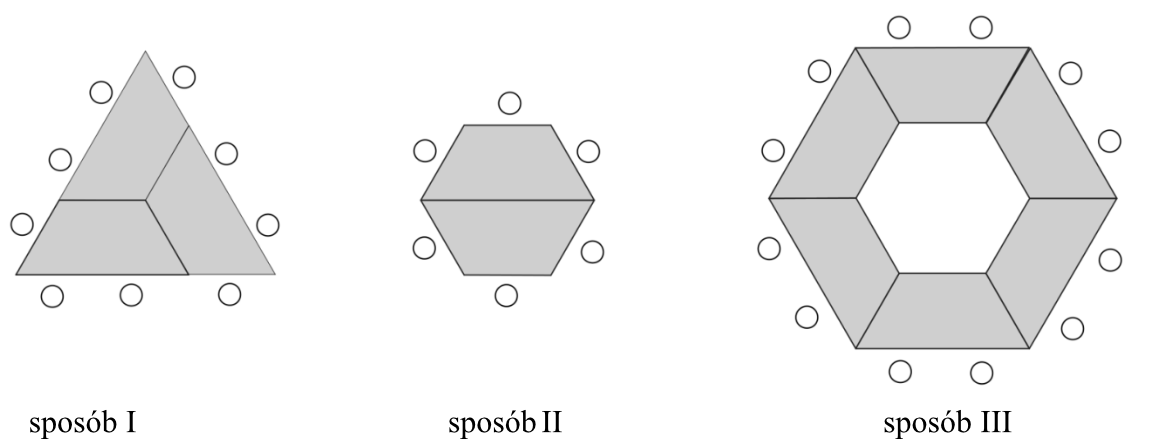
Stoliki można ze sobą łączyć na różne sposoby. Na rysunkach przedstawiono trzy przykładowe zestawienia stolików w stoły konferencyjne oraz sposoby ustawienia przy nich krzeseł.





Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. Kąty trapezu przedstawionego na rysunku 1 mają miary: \(60°, 60°, 120°, 120°\).
Krótsza podstawa tego trapezu jest \(2\) razy mniejsza od jego dłuższej podstawy.

Kąty trapezu przedstawionego na rysunku 1 mają miary: \(60°, 60°, 120°, 120°\).

Odpowiedź:      

1) PRAWDA

2) PRAWDA

Rozwiązanie:      
Krok 1. Ocena prawdziwości pierwszego zdania. To zdanie jest prawdą. Najlepiej jest to widać na pierwszym rysunku, gdzie powstał nam trójkąt równoboczny. Skąd wiemy, że ten trójkąt jest równoboczny? Każdy bok tego trójkąta składa się z jednej podstawy trapezu oraz z jednego ramienia trapezu, zatem na pewno każdy bok tego trójkąta ma jednakową miarę. Przejdźmy zatem do udowodnienia, że kąty w trapezie mają rzeczywiście miary \(60°, 60°, 120°, 120°\). Na rysunku widzimy, że jeden z kątów trapezu musi mieć miarę \(60°\), bo jeden z kątów trapezu pokrywa się z kątem trójkąta równobocznego, a jak wiemy wszystkie kąty w trójkątach równobocznych mają \(60°\). Dodatkowo musimy pamiętać, że jedną z własności trapezów jest to, że kąty przy jednym ramieniu muszą dać sumę \(180°\). W ten sposób możemy bez przeszkód określić, że kąt rozwarty w tym trapezie ma miarę \(180°-60°=120°\). Wiemy też, że jest to trapez równoramienny, więc przy jednym i drugim ramieniu kąty mają jednakową miarę, stąd też możemy być pewni, że trapez ma rzeczywiście miary kątów równe \(60°, 60°, 120°, 120°\). Krok 2. Ocena prawdziwości drugiego zdania. Najprościej będzie dostrzec to dzieląc trapez na trzy trójkąty równoboczne: Z rysunku wyraźnie wynika, że dolna podstawa trapezu ma długość \(2a\), natomiast górna podstawa ma długość \(a\), zatem zdanie jest prawdą.

Teoria:      
W trakcie opracowania