Na dwóch bokach trójkąta prostokątnego \(ABC\) zbudowano kwadraty. Pole kwadratu zbudowanego na boku \(BC\) jest równe \(169\), a pole kwadratu zbudowanego na boku \(AC\) jest równe \(25\).





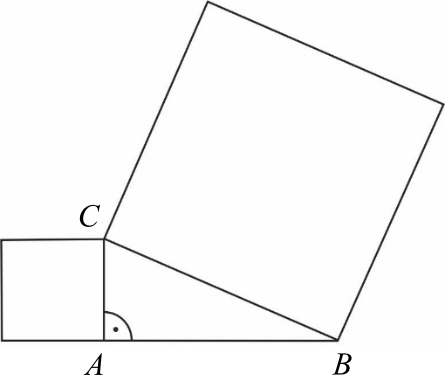
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. Bok \(BC\) ma długość \(13\).
Pole kwadratu zbudowanego na boku \(AB\) jest równe \(144\).

Bok \(BC\) ma długość \(13\).

Odpowiedź:      

1) PRAWDA

2) PRAWDA

Rozwiązanie:      
Krok 1. Ocena prawdziwości pierwszego zdania. Bok \(BC\) jest jednocześnie bokiem kwadratu o polu \(169\). Korzystając ze wzoru na pole kwadratu możemy bez problemu obliczyć tę długość: $$P=a^2 \           ,\ a^2=169 \           ,\ a=13$$ To oznacza, że faktycznie bok \(BC\) ma długość \(13\). Krok 2. Ocena prawdziwości drugiego zdania. Do odpowiedzi na to pytanie potrzebujemy poznać jeszcze długość odcinka \(AC\), którą wyliczymy dokładnie tak samo jak \(BC\), czyli korzystając ze wzoru na pole kwadratu: $$P=a^2 \           ,\ a^2=25 \           ,\ a=5$$ Wiemy już, że w tym trójkącie prostokątnym \(|AC|=5\) oraz \(|BC|=13\). Długość boku \(AB\) wyliczymy korzystając z Twierdzenia Pitagorasa: $$a^2+b^2=c^2 \           ,\ a^2+5^2=13^2 \           ,\ a^2+25=169 \           ,\ a^2=144 \           ,\ a=12$$ Skoro bok \(AB\) ma długość \(12\), to kwadrat zbudowany na tym boku będzie mieć pole powierzchni równe: $$P=a^2 \           ,\ P=12^2 \           ,\ P=144$$ Drugie zdanie jest więc prawdą.

Teoria:      
W trakcie opracowania