Trójkąt \(ABC\) jest równoboczny. Punkt \(E\) leży na wysokości \(CD\) tego trójkąta oraz \(|CE|=\frac{3}{4}|CD|\). Punkt \(F\) leży na boku \(BC\) i odcinek \(EF\) jest prostopadły do \(BC\) (zobacz rysunek).





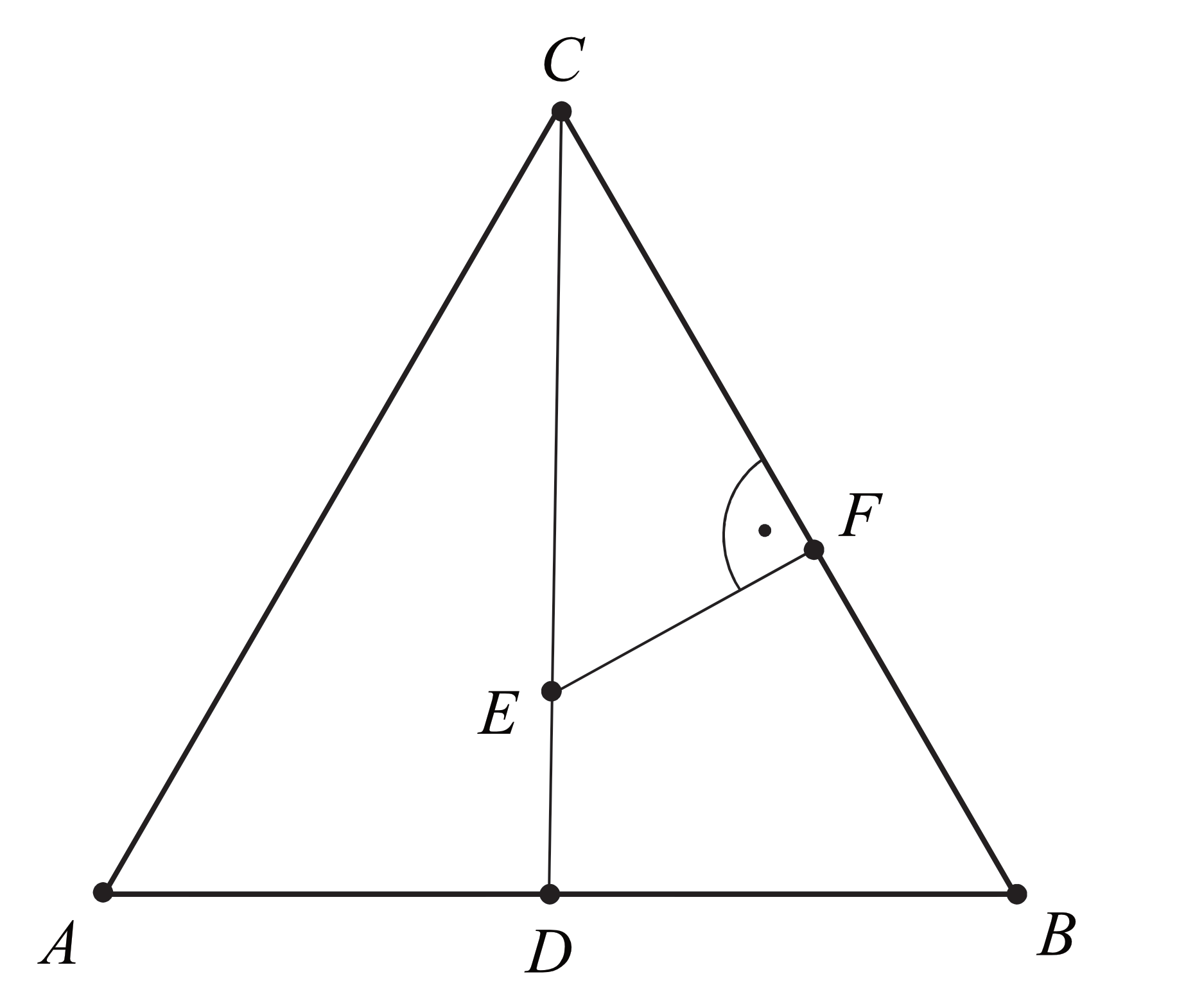
Wykaż, że \(|CF|=\frac{9}{16}|CB|\).

Odpowiedź:      

Udowodniono korzystając z własności figur podobnych.

Rozwiązanie:      
Krok 1. Rozpisanie długości odcinka \(CE\) Z własności trójkątów równobocznych wiemy, że \(h=\frac{a\sqrt{3}}{2}\). To z kolei oznacza, że \(|CD|=\frac{a\sqrt{3}}{2}\). Z treści zadania wynika, że odcinek \(CE\) stanowi \(\frac{3}{4}\) odcinka \(CD\), zatem: $$|CE|=\frac{3}{4}|CD| \           ,\ |CE|=\frac{3}{4}\cdot\frac{a\sqrt{3}}{2} \           ,\ |CE|=\frac{3\sqrt{3}a}{8}$$ Krok 2. Dostrzeżenie podobieństwa trójkątów \(CEF\) oraz \(CDB\). Spójrzmy na trójkąty \(CEF\) oraz \(CDB\). Jeden i drugi trójkąt jest prostokątny, czyli wiemy już, że na pewno mają jedną wspólną miarę kątów. Jeden i drugi trójkąt mają też wspólny kąt \(ECF\), zatem już dwa kąty w tych trójkątach są jednakowej miary. To z kolei oznacza, że i trzeci kąt w tych trójkątach musi mieć jednakową miarę. To prowadzi nas do wniosku, że zgodnie z zasadą kąt-kąt-kąt, trójkąt \(CEF\) jest podobny do trójkąta \(CDB\). Krok 3. Ułożenie równania i wyznaczenie długości odcinka \(CF\). Skoro trójkąty \(CEF\) oraz \(CDB\) są podobne, to możemy ułożyć następującą proporcję: $$\frac{|CF|}{|CD|}=\frac{|CE|}{|CB|} \           ,\ \frac{|CF|}{\frac{a\sqrt{3}}{2}}=\frac{\frac{3\sqrt{3}a}{8}}{a} \           ,\ \frac{|CF|}{\frac{a\sqrt{3}}{2}}=\frac{3\sqrt{3}}{8} \           ,\ |CF|=\frac{3\sqrt{3}}{8}\cdot\frac{a\sqrt{3}}{2} \           ,\ |CF|=\frac{3\sqrt{3}\cdot\sqrt{3}\cdot a}{8\cdot2} \           ,\ |CF|=\frac{9a}{16}=\frac{9}{16}a$$ Krok 4. Zakończenie dowodzenia. Długość \(a\) jest długością każdego z trzech boków naszego trójkąta, zatem także i boku \(BC\). Możemy więc zapisać, że z obliczeń otrzymaliśmy równanie \(|CF|=\frac{9}{16}|BC|\), czyli dokładnie takie jakie było w treści zadania. To kończy nasze dowodzenie.

Teoria:      
W trakcie opracowania