Pole prostokąta \(ABCD\) jest równe \(90\). Na bokach \(AB\) i \(CD\) wybrano – odpowiednio – punkty \(P\) i \(R\), takie, że \(\frac{|AP|}{|PB|}=\frac{|CR|}{|RD|}=\frac{3}{2}\) (zobacz rysunek).





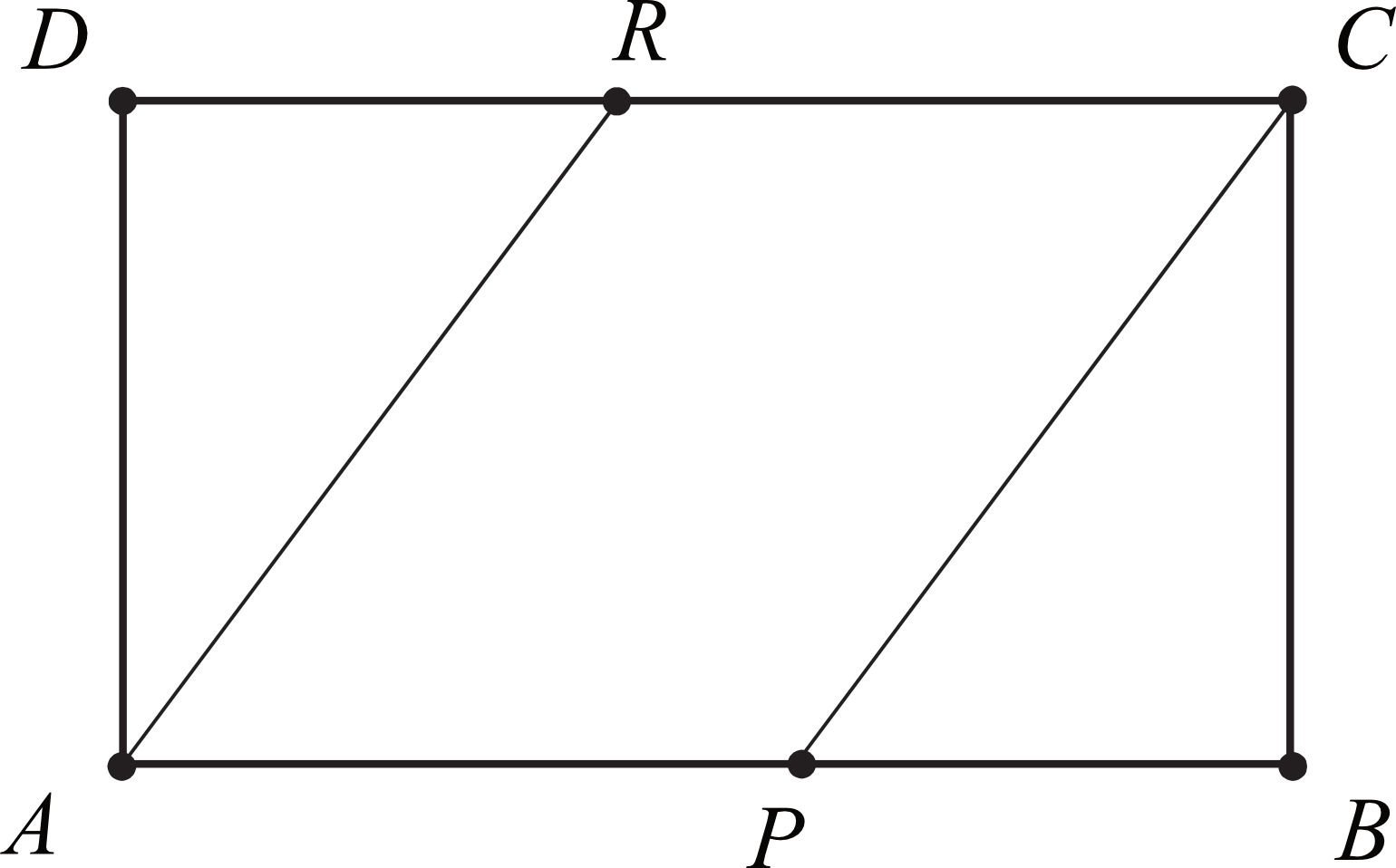
Pole czworokąta \(APCR\) jest równe:

A \(36\)
B \(40\)
C \(54\)
D \(60\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Z informacji o tym, że \(\frac{|AP|}{|PB|}=\frac{|CR|}{|RD|}=\frac{3}{2}\) wynika, że odcinki \(AP\) oraz \(RC\) mają długość \(3x\), natomiast \(PB\) oraz \(RD\) mają długość \(2x\): Dodatkowo na rysunku możemy sobie zaznaczyć, że odcinek \(AD\) jest wysokością \(h\). Krok 2. Obliczenie pola powierzchni czworokąta \(APCR\). Z treści zadania wiemy, że prostokąt \(ABCD\) o boku \(|AB|=5x\) i wysokości \(|AD|=h\) miał pole powierzchni równe \(90\). Możemy zatem zapisać, że: $$5x\cdot h=90 \           ,\ h=\frac{90}{5x}$$ Nasz równoległobok \(APCR\) będzie miał pole równe: $$P=3x\cdot h$$ Podstawiając wyznaczone przed chwilą \(h=\frac{90}{5x}\) otrzymamy: $$P=3x\cdot\frac{90}{5x} \           ,\ P=\frac{270}{5} \           ,\ P=54$$

Teoria:      
W trakcie opracowania