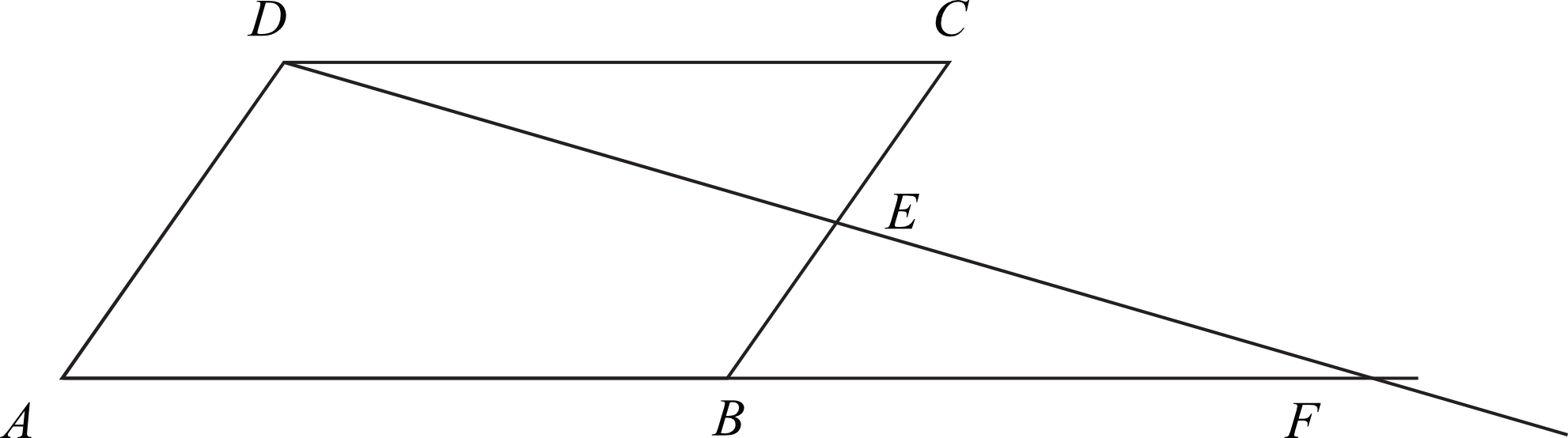
W równoległoboku \(ABCD\) punkt \(E\) jest środkiem boku \(BC\). Z wierzchołka \(D\) poprowadzono prostą przecinającą bok \(BC\) w punkcie \(E\). Proste \(AB\) i \(DE\) przecinają się w punkcie \(F\) (zobacz rysunek). Wykaż, że punkt \(B\) jest środkiem odcinka \(AF\).

Odpowiedź:      

Udowodniono korzystając z podobieństwa trójkątów.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Zgodnie z informacjami z treści zadania możemy oznaczyć sobie długości odcinków \(CE\) oraz \(EB\) jako \(x\), natomiast odcinek \(AD\) jako \(x+x=2x\). Dodatkowo oznaczmy też odcinek \(AB\) jako \(a\) oraz odcinek \(BF\) jako \(b\). Krok 2. Dostrzeżenie podobieństwa trójkątów i zapisanie równania. Trójkąty \(BFE\) oraz \(AFD\) są trójkątami podobnymi. Możemy być tego pewni, gdyż proste \(AD\) oraz \(BE\) są prostymi równoległymi (bo jest to równoległobok). Skoro tak, to możemy zapisać stosunki długości poszczególnych boków tworzą następujące równanie: $$\frac{b}{x}=\frac{a+b}{2x}$$ Krok 3. Rozwiązanie powstałego równania. Powstało nam równanie, które musimy teraz rozwiązać. Najprościej będzie zacząć od mnożenia na krzyż. Otrzymamy wtedy: $$b\cdot2x=(a+b)\cdot x \           ,\ 2bx=ax+bx \quad\bigg/-bx \           ,\ bx=ax \quad\bigg/:x \           ,\ a=b$$ Krok 4. Zakończenie dowodzenia. Udało nam się udowodnić, że odcinek \(a\) (czyli \(AB\)), jest równy odcinkowi \(b\) (czyli \(BF\)). To oznacza, że punkt \(B\) jest środkiem odcinka \(AF\), bo tylko środek odcinka może podzielić go na dwie równe części. Dowodzenie możemy uznać więc za skończone.

Teoria:      
W trakcie opracowania