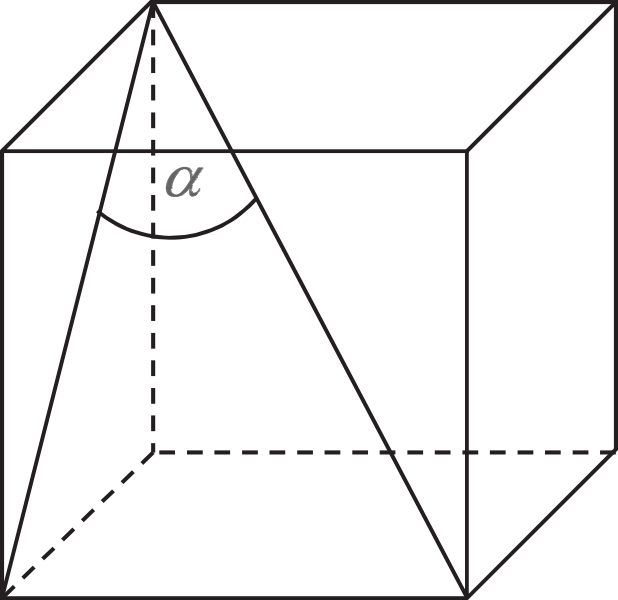
Jeżeli \(α\) oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to:

A \(sinα=\frac{\sqrt{6}}{3}\)
B \(sinα=\frac{\sqrt{2}}{2}\)
C \(sinα=\frac{\sqrt{3}}{2}\)
D \(sinα=\frac{\sqrt{3}}{3}\)

Odpowiedź:      

D

Rozwiązanie:      
Krawędź sześcianu, przekątna ściany bocznej oraz przekątna sześcianu tworzą trójkąt prostokątny. Sinus bada stosunek długości przyprostokątnej leżącej naprzeciwko kąta \(α\) (czyli w tym przypadku krawędzi podstawy) do długości przeciwprostokątnej (czyli w tym przypadku przekątnej sześcianu). Z własności sześcianu wiemy, że przekątna sześcianu o boku \(a\) ma długość \(a\sqrt{3}\), zatem: $$sinα=\frac{a}{a\sqrt{3}} \           ,\ sinα=\frac{1}{\sqrt{3}} \           ,\ sinα=\frac{1\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}} \           ,\ sinα=\frac{\sqrt{3}}{3}$$

Teoria:      
W trakcie opracowania