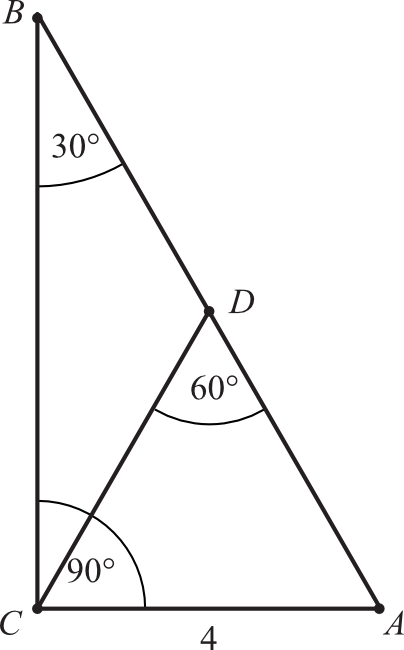
Długość odcinka \(BD\) w trójkącie prostokątnym \(ABC\) jest równa:

A \(\frac{9\sqrt{3}}{4}\)
B \(4\)
C \(4\sqrt{3}\)
D \(4\sqrt{2}\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Wyznaczenie miary kąta \(CAB\). Spójrzmy na trójkąt \(ABC\). Wiemy, że w tym trójkącie znalazły się kąty \(30°\) oraz \(90°\), zatem trzeci kąt tego trójkąta ma miarę: $$|\sphericalangle CAB|=180°-30°-90°=60°$$ Krok 2. Wyznaczenie miary kąta \(DCA\). Teraz spójrzmy na trójkąt \(CAD\). Wiemy że kąt \(CAD\) ma miarę \(60°\) (bo \(|\sphericalangle CAD|=|\sphericalangle CAB|=60°\)). Wiemy też że \(|\sphericalangle CDA|=60°\), zatem: $$|\sphericalangle DCA|=180°-60°-60°=60°$$ Możemy więc już wywnioskować, że trójkąt \(CAD\) jest trójkątem równobocznym. Krok 3. Wyznaczenie miary kąta \(BCD\). Teraz spójrzmy na kąt \(BCA\), który ma miarę \(90°\). Składa się on z kąta \(DCA\) (którego miarę obliczyliśmy przed chwilą) oraz kąta \(BCD\), który ma w takim razie ma miarę: $$|\sphericalangle BCD|=90°-60°=30°$$ To oznacza, że trójkąt \(BCD\) jest trójkątem równoramiennym o kątach przy podstawie \(30°\). Krok 4. Wyznaczenie długości odcinka \(BD\). Skoro trójkąt \(CAD\) jest równoboczny, to \(|CD|=|CA|\), czyli \(|CD|=4\). Skoro trójkąt \(BCD\) jest równoramienny, to \(|BD|=|CD|\), czyli \(|BD|=4\).

Teoria:      
W trakcie opracowania