W trójkącie równoramiennym \(ABC\) o wysokościach \(CD\) i \(AE\) podstawa \(AB\) ma długość \(8cm\), a odcinek \(BE\) ma długość \(3cm\).





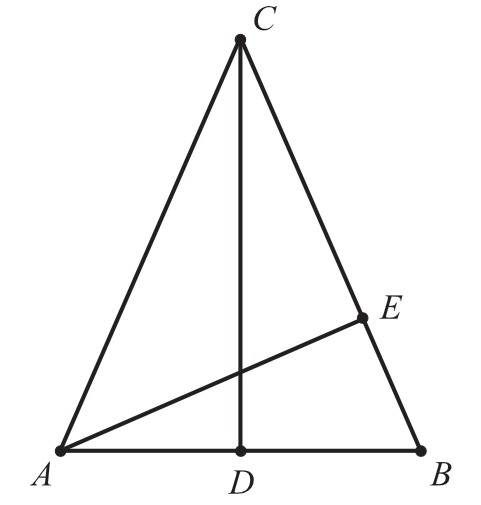
Długość odcinka \(AC\) jest równa:

A \(6cm\)
B \(\frac{32}{3}cm\)
C \(\frac{28}{3}cm\)
D \(\frac{33}{2}cm\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Oznaczmy sobie poszczególne długości na naszym rysunku: Krok 2. Obliczenie długości odcinka \(AE\). Korzystając z Twierdzenia Pitagorasa w trójkącie prostokątnym \(ABE\) możemy zapisać, że: $$|BE|^2+|AE|^2=|AB|^2 \           ,\ 3^2+|AE|^2=8^2 \           ,\ 9+|AE|^2=64 \           ,\ |AE|^2=55 \           ,\ |AE|=\sqrt{55}$$ Krok 3. Obliczene długości \(x\). Teraz spójrzmy na trójkąt prostokątny \(AEC\). Korzystając z Twierdzenia Pitagorasa możemy zapisać, że: $$|AE|^2+|EC|^2=|AC|^2 \           ,\ (\sqrt{55})^2+x^2=(x+3)^2 \           ,\ 55+x^2=x^2+6x+9 \           ,\ 46=6x \           ,\ x=\frac{46}{6}=\frac{23}{3}$$ Krok 4. Obliczenie długości odcinka \(AC\). Teraz zgodnie z oznaczeniami na rysunku możemy zapisać, że: $$|AC|=\frac{23}{3}+3 \           ,\ |AC|=\frac{23}{3}+\frac{9}{3} \           ,\ |AC|=\frac{32}{3}$$

Teoria:      
W trakcie opracowania