Punkty \(A, B, C, D, E\), leżące na okręgu o środku \(S\), są wierzchołkami pięciokąta, którego wszystkie boki mają jednakowe długości. Punkt \(P\) leży na krótszym łuku \(CD\) (jak na rysunku).





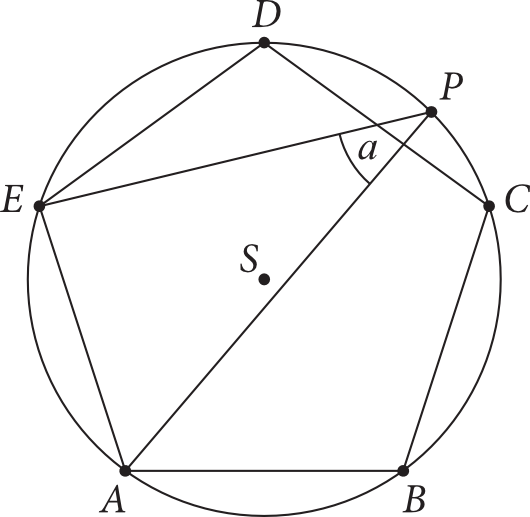
Miara \(\alpha\) kąta \(APE\) wynosi:

A \(30°\)
B \(36°\)
C \(38°\)
D \(45°\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Wyznaczenie miary kąta \(ASE\). Kąt \(ASE\) jest kątem środkowym, opartym na łuku \(AE\). Z treści zadania możemy wywnioskować, że odległość między punktami jest jednakowa (bo tylko w ten sposób powstałby nam pięciokąt o jednakowej długości boków), a to oznacza, że łuk \(AE\) stanowi \(\frac{1}{5}\) długości całego okręgu. Z własności okręgów wynika, że w takiej sytuacji kąt środkowy będzie stanowił \(\frac{1}{5}\) kąta pełnego, czyli będzie miał miarę: $$\frac{1}{5}\cdot360°=72°$$ Krok 2. Obliczenie miary kąta \(APE\). Kąt \(APE\) jest kątem wpisanym, opartym na tym samym łuku co kąt środkowy \(ASE\). Z własności kątów wpisanych i środkowych wiemy, że w takim razie miara kąta \(APE\) będzie dwa razy mniejsza od kąta \(ASE\), czyli: $$|\sphericalangle APE|=72°:2=36°$$

Teoria:      
W trakcie opracowania