Na rysunku przedstawiono wycinek koła o kącie środkowym \(120°\) i polu równym \(12\pi\).





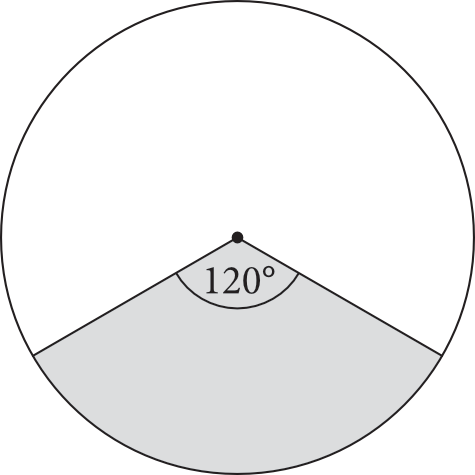
Obwód tego koła jest równy:

A \(36\pi\)
B \(12\pi\)
C \(6\pi\)
D \(4\pi\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Obliczenie pola powierzchni koła. Jeżeli kąt środkowy ma miarę \(120°\), a pełne koło ma \(360°\), to ten wycinek będzie stanowił \(\frac{120}{360}=\frac{1}{3}\) pola powierzchni koła. Skoro więc wycinek koła ma pole równe \(12\pi\), to całe koło będzie mieć powierzchnię trzy razy większą, czyli \(36\pi\). Krok 2. Obliczenie promienia koła. Korzystając ze wzoru na pole koła możemy zapisać, że: $$P=\pi r^2 \           ,\ 36\pi=\pi r^2 \           ,\ r^2=36 \           ,\ r=6 \quad\lor\quad r=-6$$ Ujemny wynik oczywiście odrzucamy, zatem zostaje nam \(r=6\). Krok 3. Obliczenie obwodu koła. Znając długość promienia \(r=6\) możemy bez problemu obliczyć obwód koła: $$Obw=2\pi r \           ,\ Obw=2\pi \cdot6 \           ,\ Obw=12\pi$$

Teoria:      
W trakcie opracowania