Ramię \(AD\) trapezu \(ABCD\) o podstawach \(AB\) i \(CD\) jest zarazem wysokością tego trapezu. Podstawa \(CD\) i ramię \(BC\) mają długości równe \(8\), a kąt między tymi bokami jest równy \(120°\) (jak na rysunku).





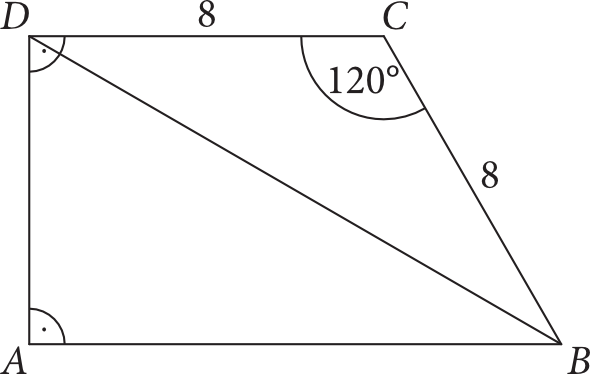
Oblicz pole trapezu \(ABCD\) oraz długość jego przekątnej \(BD\).

Odpowiedź:      

\(P=40\sqrt{3}\) oraz \(|BD|=8\sqrt{3}\)

Rozwiązanie:      
Krok 1. Obliczenie miar kątów. Możemy skorzystać z własności trapezów, która mówi nam, że kąty przy jednym ramieniu trapezu mają łączną miarę \(180°\). Skoro więc kąt \(BCD\) ma miarę \(120°\), to kąt \(ABC\) będzie miał: $$|\sphericalangle ABC|=180°-120°=60°$$ Krok 2. Sporządzenie rysunku pomocniczego. Nanosząc na rysunek odpowiednie kąty, otrzymamy taką oto sytuację: Wyszło nam, że trójkąt \(EBC\) jest trójkątem prostokątnym o kątach \(30°, 60°, 90°\) i to będzie punkt wyjścia do dalszych obliczeń. Krok 3. Obliczenie długości odcinków \(EB\) oraz \(EC\). Z własności trójkątów o kątach \(30°, 60°, 90°\) wynika, że, bok \(EB\) będzie miał miarę dwa razy krótszą od przeciwprostokątnej \(BC\), czyli że \(|EB|=4\). Dodatkowo z tych samych własności wynika, że przyprostokątna \(EC\) będzie \(\sqrt{3}\) razy dłuższa od przyprostokątnej \(EB\), czyli \(|EC|=4\sqrt{3}\). Krok 4. Obliczenie pola powierzchni trapezu. Znamy już tak naprawdę wszystkie potrzebne dane do obliczenia pola trapezu. Dolna podstawa \(AB\) będzie miała długość \(|AB|=8+4=12\), górna podstawa ma długość \(|DC|=8\), a wysokość naszego trapezu to \(|EC|=4\sqrt{3}\). Skoro tak, to: $$P=\frac{1}{2}(a+b)\cdot h \           ,\ P=\frac{1}{2}\cdot(12+8)\cdot4\sqrt{3} \           ,\ P=\frac{1}{2}\cdot20\cdot4\sqrt{3} \           ,\ P=10\cdot4\sqrt{3} \           ,\ P=40\sqrt{3}$$ Krok 5. Obliczenie długości przekątnej \(BC\). Musimy jeszcze obliczyć długość przekątnej \(BC\). Dokonamy tego korzystając z Twierdzenia Pitagorasa w trójkącie \(ABD\). Możemy zapisać, że: $$12^2+(4\sqrt{3})^2=|BD|^2 \           ,\ 144+16\cdot3=|BD|^2 \           ,\ 144+48=|BD|^2 \           ,\ |BD|^2=192 \           ,\ |BD|=\sqrt{192} \quad\lor\quad |BD|=-\sqrt{192}$$ Ujemny wynik oczywiście odrzucamy, zatem zostaje nam \(|BD|=\sqrt{192}\), co możemy jeszcze rozpisać jako \(|BD|=\sqrt{64\cdot3}=8\sqrt{3}\).

Teoria:      
W trakcie opracowania