Punkty \(A, B, P\) leżą na okręgu o środku \(S\) i promieniu \(6\). Czworokąt \(ASBP\) jest rombem, w którym kąt ostry \(PAS\) ma miarę \(60°\) (zobacz rysunek).





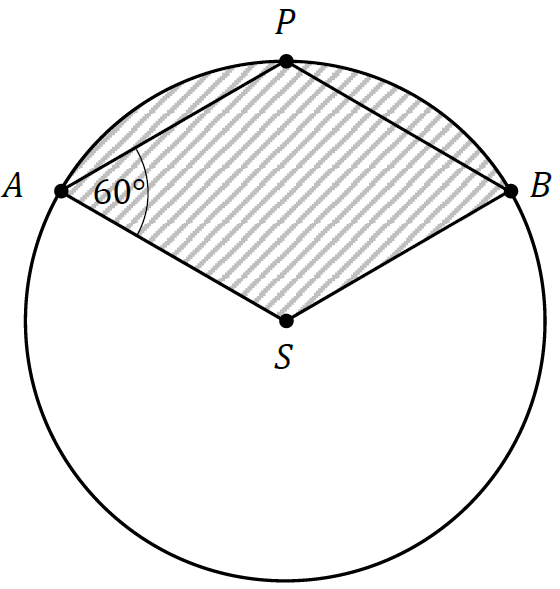
Pole zakreskowanej na rysunku figury jest równe:

A \(6\pi\)
B \(9\pi\)
C \(10\pi\)
D \(12\pi\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(ASB\). Kąty przy jednym ramieniu rombu mają łączną miarę \(180°\), a skoro tak, to: $$|\sphericalangle ASB|=180°-60°=120°$$ Krok 2. Obliczenie pola zakreskowanej figury. Zakreskowany fragment stanowi \(\frac{120°}{360°}=\frac{1}{3}\) całego koła o promieniu \(6\). Skoro tak, to możemy zapisać, że: $$P=\frac{1}{3}\cdot \pi r^2 \           ,\ P=\frac{1}{3}\cdot \pi\cdot 6^2 \           ,\ P=\frac{1}{3}\cdot36\pi \           ,\ P=12\pi$$

Teoria:      
W trakcie opracowania