Na rysunku 1. przedstawiono wykres funkcji \(f\) określonej na zbiorze \(\langle-4,5\rangle\).





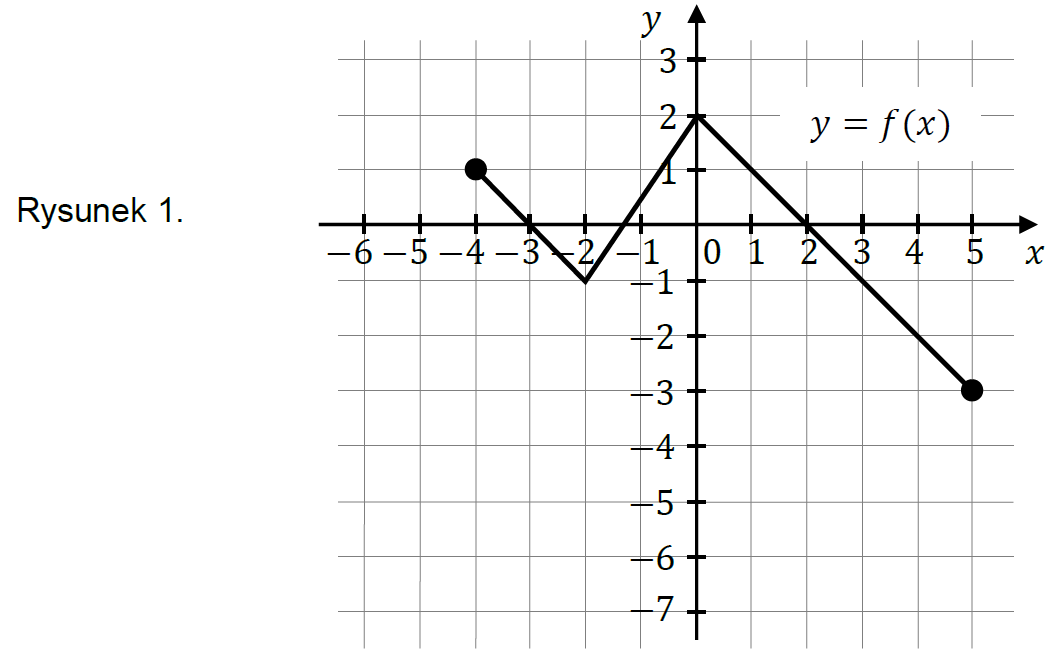
Funkcję \(g\) określono za pomocą funkcji \(f\). Wykres funkcji \(g\) przedstawiono na rysunku 2.





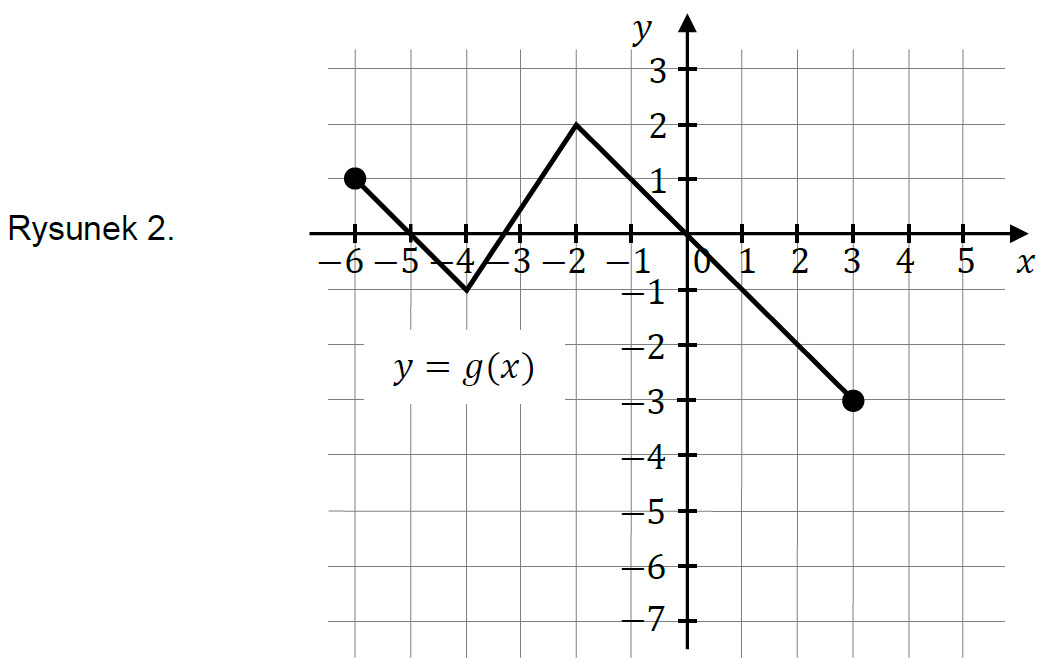
Wynika stąd, że:

A \(g(x)=f(x)-2\)
B \(g(x)=f(x-2)\)
C \(g(x)=f(x)+2\)
D \(g(x)=f(x+2)\)

Odpowiedź:      

D

Rozwiązanie:      
W tym zadaniu trzeba wykazać się wiedzą na temat przekształceń funkcji. Widzimy, że funkcja \(g(x)\) powstała w wyniku przesunięcia funkcji \(f(x)\) o \(2\) jednostki w lewo. Musimy pamiętać, że przesunięcia w lewo/prawo są tymi mniej intuicyjnymi i chcąc zapisać wzór funkcji przesuniętej w lewo, będziemy musieli dać w nawiasie znak dodawania. Skoro tak, to wzorem tej funkcji będzie \(g(x)=f(x+2)\).

Teoria:      
W trakcie opracowania